题目内容
20.已知正方形ABCD,等边三角形PAQ,其中点P在BC上,点Q在CD上,则∠BAP=( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
分析 先证明△AQD≌△APB,然后可知∠DAQ=∠BAP,再根据正方形与等边三角形的性质即可求出∠BAP的值.
解答  解:由题意可知:AD=AB,AQ=AP
解:由题意可知:AD=AB,AQ=AP
在Rt△AQD与Rt△APB中,
$\left\{\begin{array}{l}{AQ=AP}\\{AD=AB}\end{array}\right.$
∴Rt△AQD≌Rt△APB(HL)
∴∠DAQ=∠BAP,
∴∠DAQ+∠BAP=∠DAB-∠QAP=30°,
∴BAP=15°
点评 本题考查正方形的性质,涉及等边三角形的性质,全等三角形的性质与判定,角度计算问题,本题综合性较强.

练习册系列答案
相关题目
11.为纪念抗日战争胜利70周年,进一步加强爱国主义教育,某校七年级二班决定组织同学们观看爱国主义影片,已知该班$\frac{4}{5}$的学生坐在$\frac{3}{4}$的椅子上,其余的学生因为参加学校组组的合唱团而缺席,若有12张椅子是空着的,请问该班共有多少名学生( )
| A. | 55 | B. | 50 | C. | 45 | D. | 40 |
8.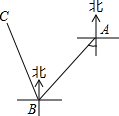 一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距( )
一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距( )
 一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距( )
一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距( )| A. | 100海里 | B. | 80海里 | C. | 60海里 | D. | 40海里 |

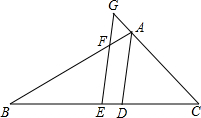 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.求证:BF=AC+AF.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.求证:BF=AC+AF. 如图,已知AB=CD,AD=BC,现有下列结论:
如图,已知AB=CD,AD=BC,现有下列结论: