题目内容
3.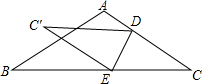 如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )| A. | 30° | B. | 60° | C. | 75° | D. | 150° |
分析 首先由邻补角的定义和四边形内角和定理得出∠C′+∠C=∠ADC′+∠BEC′,再由三角形内角和定理求出∠C=30°,即可得出答案.
解答 解:由邻补角的定义可知∠C′DC=180°-∠ADC′,∠C′EC=180°-∠BEC′=180°-40°=140°.
由四边形的内角和为360°可知;∠C′+∠C=360°-(180°-∠ADC′)-(180°-∠BEC′)=∠ADC′+∠BEC′,
∵∠A+∠B=150°,
∴∠C=180°-150°=30°,
由翻折的性质可知∠C′=∠C=30°,
∴∠ADC′+∠BEC′=2×30°=60°;
故选:B.
点评 本题主要考查的是翻折变换、邻补角的定义、四边形的内角和,掌握翻折变换的性质是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
13.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间的关系如表,下列说法不正确的是( )
| x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
| A. | x与y都是变量,且x是自变量,y是x的函数 | |
| B. | 弹簧不挂重物时的长度为0cm | |
| C. | 物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 所挂物体质量为7kg时,弹簧长度为23.5cm |
11.若关于x的不等式ax-b>0的解集为x<$\frac{1}{3}$,则关于x的不等式(a+b)x>a-b的解集为( )
| A. | x<-$\frac{1}{2}$ | B. | x$>-\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
18.为了解全校学生的视力状况,从1500名学生中抽出150名学生进行视力检测,这150名学生的视力是( )
| A. | 个体 | B. | 总体 | C. | 样本容量 | D. | 样本 |
8.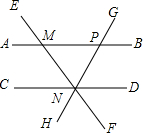 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )| A. | ∠DNG=∠AME | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠EMB=∠END |
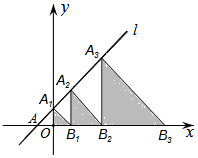 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上.若△A1OB1,△A2B1B2,△A3B2B3依次均为等腰直角三角形,直角顶点都在x轴上,则第2017个等腰直角三角形A2017B2016B2017顶点B2017的横坐标为22018-2.
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上.若△A1OB1,△A2B1B2,△A3B2B3依次均为等腰直角三角形,直角顶点都在x轴上,则第2017个等腰直角三角形A2017B2016B2017顶点B2017的横坐标为22018-2.