题目内容
8.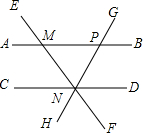 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )| A. | ∠DNG=∠AME | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠EMB=∠END |
分析 根据平行线的性质,找出各相等的角,再去对照四个选项即可得出结论.
解答 解:A、∠DNG与∠AME没有关系,无法判定其是否相等.
B、∵AB∥CD,
∴∠BMN=∠MNC(两直线平行,内错角相等);
C、∵AB∥CD,
∴∠CNH=∠MPN(两直线平行,同位角相等),
∵∠MPN=∠BPG(对顶角),
∴∠CNH=∠BPG(等量代换);
D、∵AB∥CD,
∴∠EMB=∠END(两直线平行,同位角相等);
故选:A.
点评 本题考查了平行线的性质,解题的关键是结合平行线的性质来对照四个选择.解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
相关题目
18.已知点A(2-m,-3-n)在第二象限,则点B(m,n)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.下列各数中,无理数是( )
| A. | $\sqrt{36}$ | B. | $\sqrt{7}$ | C. | $\frac{22}{7}$ | D. | 3.141 |
3.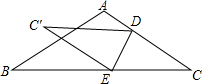 如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
 如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )| A. | 30° | B. | 60° | C. | 75° | D. | 150° |
13.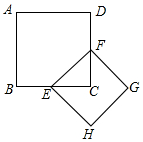 如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
 如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$+1 | D. | 2$\sqrt{2}$ |
20.下列运算正确的是( )
| A. | m3•m3=2m3 | B. | 5m2n-4mn2=mn | C. | (m+1)(m-1)=m2-1 | D. | (m-n)2=m2-mn+n2 |

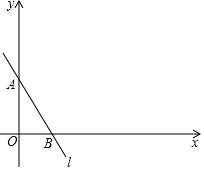 如图,已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
如图,已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.