题目内容
14.某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.(1)小丽参加实验A考查的概率是$\frac{1}{2}$;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是$\frac{1}{8}$.
分析 (1)由可参加实验考查只有两个,可得出小丽参加实验A考查的概率是$\frac{1}{2}$;
(2)画出树状图,结合树状图得出结论;
(3)由每人选择实验A考查的概率为$\frac{1}{2}$,利用概率公式即可求出三人都参加实验A考查的概率.
解答 解:(1)小丽参加实验A考查的概率是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
(2)画树状图如图所示.
∵两人的参加实验考查共有四种等可能结果,而两人均参加实验A考查有1种,
∴小明、小丽都参加实验A考查的概率为$\frac{1}{4}$.
(3)他们三人都参加实验A考查的概率是$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查了列表法与树状图法以及概率公式,解题的关键是:(1)根据可参加的实验考查的个数,求出小丽参加实验A考查的概率;(2)画出树状图;(3)套用概率公式求出三人都参加实验A考查的概率.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.方程组$\left\{\begin{array}{l}{2x+y=□}\\{x+y=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=△}\end{array}\right.$,则被遮盖的两个数△,□分别为( )
| A. | 1,2 | B. | 1,3 | C. | 1,5 | D. | 2,4 |
3.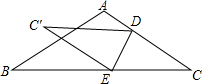 如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
 如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )
如图,将一张三角形纸片ABC沿DE折叠,点C落在点C′处,若∠A+∠B=150°,则∠ADC′+∠BEC′的值为( )| A. | 30° | B. | 60° | C. | 75° | D. | 150° |