Question

10．梯形ABCD中，AB∥CD，E、F分别为两腰AD、BC上的点，且EF∥AB，设AB=a，CD=b（a＜b），且S_梯形ABFE：S_梯形EFCD=m：n，则EF=$\frac{\sqrt{（m+n）（m{b}^{2}+n{a}^{2}）}}{m+n}$．

Answer 1

分析 先作辅助线，构建平行四边形和梯形的高线，设EG=x，AM=h₁，MN=h₂，因为EG∥DH得△AEG∽△ADH，根据相似三角形对应边的比等于对应高的比得$\frac{EG}{DH}=\frac{AM}{AN}$，代入求出$\frac{{h}_{1}}{{h}_{2}}$=$\frac{x}{b-a-x}$，再由已知的S_梯形ABFE：S_梯形EFCD=m：n代入得：（m+n）EF²=a²n+b²m，解方程即可．

解答 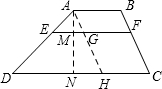解：过A作AH∥BC，交DC于H，交EF于G，得?AGFB、?GHCF，
∴FG=HC=AB=a，
过A作AN⊥DC于N，交EF于M，则AN⊥EF，
设EG=x，AM=h₁，MN=h₂，
∵EG∥DH，
∴△AEG∽△ADH，
∴$\frac{EG}{DH}=\frac{AM}{AN}$，
∴$\frac{x}{b-a}=\frac{{h}_{1}}{{h}_{1}+{h}_{2}}$，
∴$\frac{{h}_{1}}{{h}_{2}}$=$\frac{x}{b-a-x}$，
∵S_梯形ABFE：S_梯形EFCD=m：n，
∴$\frac{\frac{1}{2}（AB+EF）•{h}_{1}}{\frac{1}{2}（DC+EF）•{h}_{2}}$=$\frac{m}{n}$，
∴$\frac{AB+EF}{DC+EF}$•$\frac{x}{b-a-x}$=$\frac{m}{n}$，
∴$\frac{（a+EF）（EF-a）}{（b+EF）（b-EF）}$=$\frac{m}{n}$，
（m+n）EF²=a²n+b²m，
∵EF＞0，
∴EF=$\sqrt{\frac{m{b}^{2}+n{a}^{2}}{m+n}}$=$\frac{\sqrt{（m+n）（m{b}^{2}+n{a}^{2}）}}{m+n}$．
故答案为：$\frac{\sqrt{（m+n）（m{b}^{2}+n{a}^{2}）}}{m+n}$．

点评 此题考查了梯形、平行四边形以及相似三角形的判定与性质，注意准确作出辅助线是解此题的关键；巧妙的设未知数，表示其它边的长度，代入S_梯形ABFE：S_梯形EFCD=m：n中，即可得出结论．