题目内容
8.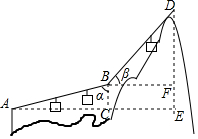 如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.(参考数据:sin75°≈0.97,cos75°≈0.26,$\sqrt{2}$≈1.41)
分析 在R△ABC中,求出BC=AB•cos75°≈600×0.26≈156m,在Rt△BDF中,求出DF=BD•sin45°=600×$\frac{\sqrt{2}}{2}$≈300×1.41≈423,由四边形BCEF是矩形,可得EF=BC,由此即可解决问题.
解答 解:在Rt △ABC中,∵AB=600m,∠ABC=75°,
△ABC中,∵AB=600m,∠ABC=75°,
∴BC=AB•cos75°≈600×0.26≈156m,
在Rt△BDF中,∵∠DBF=45°,
∴DF=BD•sin45°=600×$\frac{\sqrt{2}}{2}$≈300×1.41≈423,
∵四边形BCEF是矩形,
∴EF=BC=156,
∴DE=DF+EF=423+156=579m.
答:DE的长为579m.
点评 本题考查解直角三角形的应用,锐角三角函数、矩形的性质等知识,解题的关键是学会利用直角三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列计算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | a2+a4=a6 | C. | (-$\frac{1}{3}$)-1=$\frac{1}{3}$ | D. | (-π)0=1 |
16.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=$\frac{9}{2}$;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.不等式4-2x>0的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
9.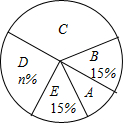 某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
根据以上信息,解答下列问题:
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有18人,这些学生数占被调查总人数的百分比为15%,每天参加体育锻炼的时间不足60min的有30人;
(2)被调查的学生总数为120人,统计表中m的值为42,统计图中n的值为25,被调查学生每天参加体育锻炼时间的中位数落在C组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
 某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.| 组别 | A | B | C | D | E |
| 时间t/min | t<45 | 45≤t<60 | 60≤t<75 | 75≤t<90 | t≥90 |
| 人数 | 12 | 18 | m | 30 | 18 |
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有18人,这些学生数占被调查总人数的百分比为15%,每天参加体育锻炼的时间不足60min的有30人;
(2)被调查的学生总数为120人,统计表中m的值为42,统计图中n的值为25,被调查学生每天参加体育锻炼时间的中位数落在C组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
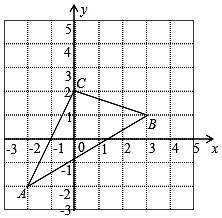 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中