题目内容
10.化简:(1)($\sqrt{a+b}$)2=a+b;$\sqrt{(a+b)^{2}}$=|a+b|;
(2)($\root{3}{abc+1}$)3-$\root{3}{(abc+1)^{3}}$=0.
分析 (1)根据$\sqrt{{a}^{2}}$=|a|,($\sqrt{a}$)2=a,进行计算即可.
(2)根据$\root{3}{{a}^{3}}$=a,($\root{3}{a}$)3=a进行计算即可.
解答 解:(1)($\sqrt{a+b}$)2=a+b;
$\sqrt{(a+b)^{2}}$=|a+b|,
故答案为:a+b;|a+b|;
(2)($\root{3}{abc+1}$)3-$\root{3}{(abc+1)^{3}}$=abc+1-(abc+1)=abc+1-abc-1=0,
故答案为:0.
点评 此题主要考查了实数的运算,关键是掌握二次根式的性质.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,△ABC中,BD:DC=5:3,E为AD的中点,求BE:EF的值.
如图,△ABC中,BD:DC=5:3,E为AD的中点,求BE:EF的值.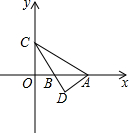 如图,在平面直角坐标系中,点A,点B在x轴上,点C在y轴上,∠ADC=90°,AB=BC,线段BC,OB的长是一元二次方程x2-6x+8=0的两根.
如图,在平面直角坐标系中,点A,点B在x轴上,点C在y轴上,∠ADC=90°,AB=BC,线段BC,OB的长是一元二次方程x2-6x+8=0的两根.