题目内容
5.(1)设x-2<7,则x<9;(2)设x+5<-3,则x<-8;
设$\frac{5-x}{2}$>$\frac{1}{3}$,则x<$\frac{13}{3}$;
(4)2x-3<7,则x<5.
分析 (1)、(2)先移项,再合并同类项即可;
(3)先去分母,再去括号,移项,合并同类项,把x的系数化为1即可;
(4)先移项,再合并同类项,把x的系数化为1即可.
解答 解:(1)移项得,x<7+2,
合并同类项得,x<9.
故答案为:9;
(2)移项得,x<-3-5,
合并同类项得,x<-8.
故答案为:-8;
(3)去分母得,3(5-x)>2,
去括号得,15-3x>2,
移项得,-3x>2-15,
合并同类项得,-3x>-13,
x的系数化为1得,x<$\frac{13}{3}$.
故答案为:$\frac{13}{3}$;
(4)移项得,2x<7+3,
合并同类项得,2x<10,
x的系数化为1得,x<5.
故答案为:5.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
15. 如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )
如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )
 如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )
如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )| A. | y=-$\frac{\sqrt{3}}{2}$x | B. | y=-$\frac{\sqrt{3}}{3}x$ | C. | y=-$\frac{1}{2}x$ | D. | y=-x |
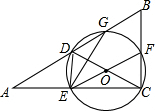 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.