题目内容
20．已知a为实数，且满足等式$\sqrt{a-2}$+|$\sqrt{3}$-a|=a，先确定a的取值范围再求a．分析 根据二次根式有意义的条件可得a的范围，结合a的范围将原式化简可得$\sqrt{a-2}$=$\sqrt{3}$，从而得出a的值．
解答 解：根据题意知，$\left\{\begin{array}{l}{a-2≥0}\\{a≥0}\end{array}\right.$，
解得：a≥2，
当a≥2时，原式可变形为$\sqrt{a-2}$+a-$\sqrt{3}$=a，
即$\sqrt{a-2}$=$\sqrt{3}$，
解得：a=5．
点评 本题主要考查二次根式有意义的条件及绝对值性质，根据二次根数有意义条件化简原式是解题的关键．
练习册系列答案
相关题目
10．
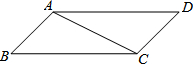如图，△ABC≌△CDA，且AB、CD是对应边，下面四个结论中不正确的是（ ）
如图，△ABC≌△CDA，且AB、CD是对应边，下面四个结论中不正确的是（ ）| A． | △ABC和△CDA的面积相等 | B． | △ABC和△CDA的周长相等 | ||
| C． | ∠B+∠BAC=∠D+∠DAC | D． | AD=BC |
完成下列证明过程．
15．
如图，菱形OABC的顶点O为坐标原点，顶点A在x轴正半轴上，顶点B、C在第一象限，OA=2，∠AOC=60°，点D在边AB上，将四边形ODBC沿直线OD翻折，使点B和点C分别落在这个坐标平面内的B′和C′处，且∠C′DB′=60°，某正比例函数图象经过B′，则这个正比例函数的解析式为（ ）
如图，菱形OABC的顶点O为坐标原点，顶点A在x轴正半轴上，顶点B、C在第一象限，OA=2，∠AOC=60°，点D在边AB上，将四边形ODBC沿直线OD翻折，使点B和点C分别落在这个坐标平面内的B′和C′处，且∠C′DB′=60°，某正比例函数图象经过B′，则这个正比例函数的解析式为（ ）| A． | y=-$\frac{\sqrt{3}}{2}$x | B． | y=-$\frac{\sqrt{3}}{3}x$ | C． | y=-$\frac{1}{2}x$ | D． | y=-x |