题目内容
16.实践操作题如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(3a+b)(2a+2b),在下面虚框③中画出图形,并根据图形回答(3a+b)(2a+2b)=6a2+8ab+2b2;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.根据你所拼成的长方形可知,多项式a2+5ab+6b2可以分解因式为(a+2b)(a+3b);
(3)若现在有3张A类纸片,6张B类纸片,10张C类纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形,则拼成的正方形边长最长可以是a+3b;
(4)若取其中的六张B类卡片拼成一个如图 ④所示的长方形,通过不同方法计算阴影部分的面积,你能得到什么等式?并用乘法法则说明这个等式成立.

分析 (1)画出图形,结合图形和面积公式得出即可;
(2)根据图形和面积公式得出即可;
(3)由完全平方公式可得三种纸片拼出一个正方形,可以让正方形的边长分别为a+b,a+2b,a+3b,由此即可确定拼出的正方形的边长最长是多少;
(4)用两种方法求出阴影部分的面积,即整个矩形面积减去6个B类卡片和阴影部分矩形的面积列式即可.
解答 解:(1)如图: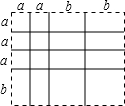
(3a+b)(2a+2b)=6a2+8ab+2b2;
(2)a2+5ab+6b2=(a+2b)(a+3b);
(3)∵有3张A类纸片,6张B类纸片,10张C类纸片,
∴由完全平方公式可得每种纸片至少取一张,把取出的这些纸片拼成一个正方形,可以让正方形的边长分别为a+b,a+2b,a+3b,
所以拼出的正方形的边长最长可以为a+3b;
(4)整个矩形面积为:(a+2b)(a+b),6个B类卡片的面积为:6ab,
阴影部分矩形的面积为:(2b-a)(b-a),
(a+2b)(a+b)-6ab=a2+2b2-3ab,
(2b-a)(b-a)=a2+2b2-3ab,
∴(a+2b)(a+b)-6ab=(2b-a)(b-a),
故答案为:6a2+8ab+2b2;(a+2b)(a+3b);a+3b.
点评 本题考查了分解因式的应用,长方形的面积,完全平方公式的应用,主要考查学生的观察图形的能力和化简能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
8.方程$\frac{1}{1-x}+\frac{x}{x-1}$=-1的解是( )
| A. | x=2 | B. | x=1 | C. | x=0 | D. | 无实数解 |
8.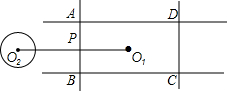 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
6. 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 3 | D. | 无法确定 |
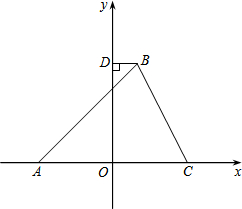 如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4$\sqrt{5}$,∠BAC=45°.
如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4$\sqrt{5}$,∠BAC=45°.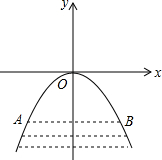 某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.
某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.
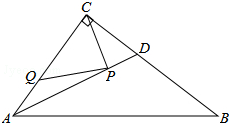 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.