题目内容
1.(1)请在图①中作出两条线,使它们将圆面四等分;(2)如图②,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=a,CD=b,且b>a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,请说明理由
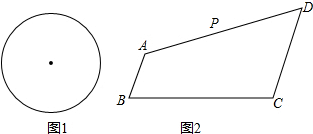
分析 (1)画出互相垂直的两直径即可;
(2)当BQ=CD=b时,PQ将四边形ABCD的面积二等份,连接BP并延长交CD的延长线于点E,证△ABP≌△DEP求出BP=EP,连接CP,求出S△BPC=S△EPC,作PF⊥CD,PG⊥BC,由BC=AB+CD=DE+CD=CE,求出S△BPC-S△CQP+S△ABP=S△CPE-S△DEP+S△CQP,即可得出S四边形ABQP=S四边形CDPQ即可.
解答 解:(1)如图1所示,
(2)存在,当BQ=CD=b时,PQ将四边形ABCD的面积二等份,
理由是:如图2,连接BP并延长交CD的延长线于点E,
∵AB∥CD,
∴∠A=∠EDP,
在△ABP和△DEP中,
$\left\{\begin{array}{l}{∠A=∠EDP}\\{AP=DP}\\{∠APB=∠DPE}\end{array}\right.$,
∴△ABP≌△DEP(ASA),
∴BP=EP,
连接CP,
∵△BPC的边BP和△EPC的边EP上的高相等,
又∵BP=EP,
∴S△BPC=S△EPC,
作PF⊥CD,PG⊥BC,则BC=AB+CD=DE+CD=CE,
由三角形面积公式得:PF=PG,
在CB上截取CQ=DE=AB=a,则S△CQP=S△DEP=S△ABP
∴S△BPC-S△CQP+S△ABP=S△CPE-S△DEP+S△CQP
即:S四边形ABQP=S四边形CDPQ,
∵BC=AB+CD=a+b,
∴BQ=b,
∴当BQ=b时,直线PQ将四边形ABCD的面积分成相等的两部分.
点评 本题考查了应用作图与设计、三角形的面积等知识点的应用,主要考查学生综合运用性质进行推理的能力,注意:等底等高的三角形的面积相等.

练习册系列答案
相关题目
9.当代数式x2+3x+8的值等于7时,代数式3x2+9x-2的值等于( )
| A. | 5 | B. | 3 | C. | -2 | D. | -5 |
 如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
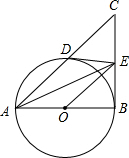 如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE
如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE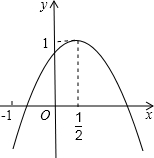 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )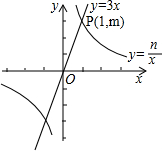 如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1.
如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1.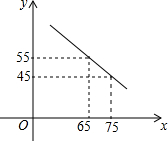 某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.
某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.