题目内容
8.方程$\frac{1}{1-x}+\frac{x}{x-1}$=-1的解是( )| A. | x=2 | B. | x=1 | C. | x=0 | D. | 无实数解 |
分析 根据分式方程的解法,去分母转化为整式方程,求出解后检验即可.
解答 解:去分母,方程两边都乘以(x-1)得,
-1+x=-(x-1)
解这个方程得:x=1,
检验:当x=1时,x-1=0,所以x=1不是原方程的解,
所以原方程无解.
故选:D.
点评 本题主要考查了分式方程的解法,注意解分式方程一定要检验.

练习册系列答案
相关题目
19.在平面直角坐标系中,抛物线y=x2-1与x轴的交点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
3.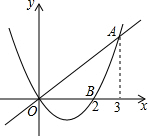 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
17.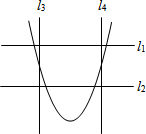 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
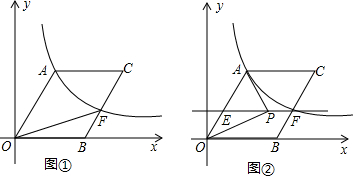
 如图,已知长方形ABCD,AB=CD=4,BC=AD=6,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A→B→C→E运动到E点停止,设点P经过的路程为x,△APE的面积为y.
如图,已知长方形ABCD,AB=CD=4,BC=AD=6,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A→B→C→E运动到E点停止,设点P经过的路程为x,△APE的面积为y. 如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.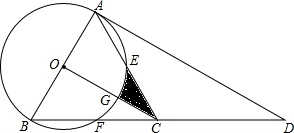 如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F