题目内容
求证:对任何整数a,a4n+k与ak的个位数字相同(n、k都是整数).
考点:尾数特征
专题:
分析:由于一个整数n次方的尾数等于其尾数n次方的尾数,所以先分别计算0-9的n次方尾数变化规律,发现0-9的n次方的尾数均遵循周期为4的循环规律,即可得证.
解答:解:∵0的任何次方都是0,遵循周期为1的循环规律,
1的任何次方都是1,遵循周期为1的循环规律,
21=2,22=4,23=8,24=16,25=32,…,即2的n次方的尾数依次为2,4,8,6,…,遵循周期为4的循环规律,
31=3,32=9,33=27,34=81,35=243,…,即3的n次方的尾数依次为3,9,7,1,…,遵循周期为4的循环规律,
41=4,42=16,43=64,44=256,45=1024,…,即4的n次方的尾数依次为4,6,…,遵循周期为2的循环规律,
5的任何次方尾数都是5,遵循周期为1的循环规律,
6的任何次方尾数都是6,遵循周期为1的循环规律,
71=7,72=49,73=343,74=2401,75=16807,…,即7的n次方的尾数依次为7,9,3,1,…,遵循周期为4的循环规律,
81=8,82=64,83=512,84=4096,85=32768,…,即8的n次方的尾数依次为8,4,2,6,…,遵循周期为4的循环规律,
91=9,92=81,93=729,94=6561,…,即9的n次方的尾数依次为9,1,…,遵循周期为2的循环规律,
∴0-9的n次方的尾数均遵循周期为4的循环规律,
又∵任何一个整数n次方的尾数等于其尾数n次方的尾数,
∴对任何整数a,a4n+k与ak的个位数字相同(n、k都是整数).
1的任何次方都是1,遵循周期为1的循环规律,
21=2,22=4,23=8,24=16,25=32,…,即2的n次方的尾数依次为2,4,8,6,…,遵循周期为4的循环规律,
31=3,32=9,33=27,34=81,35=243,…,即3的n次方的尾数依次为3,9,7,1,…,遵循周期为4的循环规律,
41=4,42=16,43=64,44=256,45=1024,…,即4的n次方的尾数依次为4,6,…,遵循周期为2的循环规律,
5的任何次方尾数都是5,遵循周期为1的循环规律,
6的任何次方尾数都是6,遵循周期为1的循环规律,
71=7,72=49,73=343,74=2401,75=16807,…,即7的n次方的尾数依次为7,9,3,1,…,遵循周期为4的循环规律,
81=8,82=64,83=512,84=4096,85=32768,…,即8的n次方的尾数依次为8,4,2,6,…,遵循周期为4的循环规律,
91=9,92=81,93=729,94=6561,…,即9的n次方的尾数依次为9,1,…,遵循周期为2的循环规律,
∴0-9的n次方的尾数均遵循周期为4的循环规律,
又∵任何一个整数n次方的尾数等于其尾数n次方的尾数,
∴对任何整数a,a4n+k与ak的个位数字相同(n、k都是整数).
点评:本题考查了整数的尾数特征,难度中等,通过计算发现0-9的n次方的尾数均遵循周期为4的循环规律是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将点P(4,3)向下平移1个单位后,落在反比例函数y=
的图象上,则k的值为( )
| k |
| x |
| A、12 | B、10 | C、9 | D、8 |
已知
+|3x-2y-a|=0,y为负数,则a的取值范围为( )
| x-2 |
| A、a≥2 | B、a<3 |
| C、a>6 | D、a≥5 |
 如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是( )
如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是( )| A、50° | B、60° |
| C、70° | D、80° |
 将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=
将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=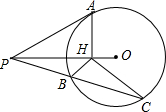 如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算
如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算 如图,在?ABCD中,E是CD上的一个动点(不与C、D重合),BE的延长线交AD的延长线于点F,则图中共有
如图,在?ABCD中,E是CD上的一个动点(不与C、D重合),BE的延长线交AD的延长线于点F,则图中共有 已知直角三角形ABC中,∠C=90°,AC=a,BC=2a.在AC、BC上分别有一动点P、Q,且PQ始终平分△ABC的面积.作PR⊥CA交AB于R,QS⊥BC交AB于S.线段BS、SR、RA能否构成一个直角三角形,证明你的猜想.
已知直角三角形ABC中,∠C=90°,AC=a,BC=2a.在AC、BC上分别有一动点P、Q,且PQ始终平分△ABC的面积.作PR⊥CA交AB于R,QS⊥BC交AB于S.线段BS、SR、RA能否构成一个直角三角形,证明你的猜想.