题目内容
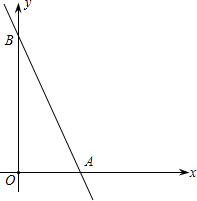 已知直线y=-2x+6交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B两点及x轴上另一点C,且AC=2.
已知直线y=-2x+6交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B两点及x轴上另一点C,且AC=2.(1)当tan∠BCO<tan∠BAO时,求抛物线的解析式.
(2)点D的坐标是(-2,0),在直线y=-2x+6上确定点P,使以点A、P、D为顶点的三角形与△ABO相似.
(3)在(1)、(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据tan∠BCO<tan∠BAO,则B在A的右侧,求出A、B、C的坐标,利用待定系数法求出函数解析式即可;
(2)作出△ADP,根据相似三角形的性质,求出AP的长,再根据等积法求出P点横纵坐标,即可求出P点坐标;
(3)根据△ADE的面积等于四边形APCE的面积,求出E的纵坐标,由于其小于顶点坐标,故E不存在.
(2)作出△ADP,根据相似三角形的性质,求出AP的长,再根据等积法求出P点横纵坐标,即可求出P点坐标;
(3)根据△ADE的面积等于四边形APCE的面积,求出E的纵坐标,由于其小于顶点坐标,故E不存在.
解答: 解:(1)∵直线y=-2x+6交x轴于点A,交y轴于点B,
解:(1)∵直线y=-2x+6交x轴于点A,交y轴于点B,
∴A、B点坐标分别为(3,0),(0,6),
∵tan∠BCO<tan∠BAO,
∴C在A的右侧,
又∵AC=2,A点坐标为(3,0),
∴C点坐标为(5,0),
如图1:设函数解析式为y=a(x-3)(x-5)
将B(0,6)代入解析式得,6=a(0-3)(0-5),
整理得,a=
,函数解析式为y=
x2-
x+6.
(2)①如图2,当△DPA∽△BOA时,
∵AO=3,BO=6,
∴AB=
=
=3
,
=
,
即
=
,
AP=
,
在△APD中,DP=
=
=2
,
设P点纵坐标为y,
×5y=
×
×2
,解得y=2,
把y=2代入y=-2x+6得,2=-2x+6,
x=2,
则P点坐标为(2,2).
②如图3,△DPA∽△OBA时,
=
,即
=
,
解得PD=10,
将PD=10代入y=-2x+6得,
-2x+6=10,解得x=-2,
则P点坐标为(-2,10).
故点P坐标为(2,2)或(-2,10).
(3)如图4:设E点坐标为|y|,
S△ADE=
×5|y|=
;
S四边形PAEC=S△PAC+S△ACE=
×2×2+
×2×|y|,
则
=
×2×2+
×2×|y|,
解得|y|=
,
即y=-
.
∵y=
x2-
x+6的顶点纵坐标为
=-
,
∵-
<-
,
∴不存在点E.
 如图5:设E点坐标为|y|,
如图5:设E点坐标为|y|,
S△ADE=
×5|y|=
;
S四边形PAEC=S△PAC+S△ACE=
×2×10+
×2×|y|,
则
=
×2×10+
×2×|y|,
解得y=-
,
∵-
<-
,
∴不存在点E.
 解:(1)∵直线y=-2x+6交x轴于点A,交y轴于点B,
解:(1)∵直线y=-2x+6交x轴于点A,交y轴于点B,∴A、B点坐标分别为(3,0),(0,6),
∵tan∠BCO<tan∠BAO,
∴C在A的右侧,
又∵AC=2,A点坐标为(3,0),
∴C点坐标为(5,0),
如图1:设函数解析式为y=a(x-3)(x-5)
将B(0,6)代入解析式得,6=a(0-3)(0-5),
整理得,a=
| 2 |
| 5 |
| 2 |
| 5 |
| 16 |
| 5 |
(2)①如图2,当△DPA∽△BOA时,

∵AO=3,BO=6,
∴AB=
| 32+62 |
| 45 |
| 5 |
| AP |
| AO |
| AD |
| AB |
即
| AP |
| 3 |
| 5 | ||
3
|
AP=
| 5 |
在△APD中,DP=
| AD2-AP2 |
52-(
|
| 5 |
设P点纵坐标为y,
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
把y=2代入y=-2x+6得,2=-2x+6,

x=2,
则P点坐标为(2,2).
②如图3,△DPA∽△OBA时,
| AO |
| AD |
| OB |
| PD |
| 3 |
| 5 |
| 6 |
| PD |
解得PD=10,
将PD=10代入y=-2x+6得,
-2x+6=10,解得x=-2,
则P点坐标为(-2,10).
故点P坐标为(2,2)或(-2,10).
(3)如图4:设E点坐标为|y|,
S△ADE=
| 1 |
| 2 |
| 5|y| |
| 2 |

S四边形PAEC=S△PAC+S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
则
| 5|y| |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得|y|=
| 4 |
| 3 |
即y=-
| 4 |
| 3 |
∵y=
| 2 |
| 5 |
| 16 |
| 5 |
4×
| ||||
4×
|
| 2 |
| 5 |
∵-
| 4 |
| 3 |
| 2 |
| 5 |
∴不存在点E.
 如图5:设E点坐标为|y|,
如图5:设E点坐标为|y|,S△ADE=
| 1 |
| 2 |
| 5|y| |
| 2 |
S四边形PAEC=S△PAC+S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
则
| 5|y| |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得y=-
| 20 |
| 3 |
∵-
| 20 |
| 3 |
| 2 |
| 5 |
∴不存在点E.
点评:本题考查了待定系数法求函数解析式、相似三角形的性质、二次函数的性质等知识,综合性很强,主要考查同学们的逻辑思维能力.

练习册系列答案
相关题目
下列计算错误的是( )
| A、(-x)9÷(-x)3=x6 |
| B、-a2•a=-a3 |
| C、(-2x)3=-2x3 |
| D、(-2a3)2=4a6 |
已知
+|3x-2y-a|=0,y为负数,则a的取值范围为( )
| x-2 |
| A、a≥2 | B、a<3 |
| C、a>6 | D、a≥5 |
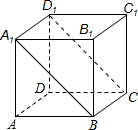 如图在棱长为1的正方体ABCD-A1B1C1D1中,一只蚂蚁从点A出发,沿正方体表面爬行到面对角线A1B上的一点P,再沿截面A1BCD1爬行到点D1,则整个过程中蚂蚁爬行的最短路程为( )
如图在棱长为1的正方体ABCD-A1B1C1D1中,一只蚂蚁从点A出发,沿正方体表面爬行到面对角线A1B上的一点P,再沿截面A1BCD1爬行到点D1,则整个过程中蚂蚁爬行的最短路程为( )| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
已知
=
,
=
,
=
,则
=( )
| xy |
| x+y |
| 1 |
| 3 |
| yz |
| y+z |
| 1 |
| 5 |
| zx |
| z+x |
| 1 |
| 6 |
| xyz |
| xy+yz+zx |
A、
| ||
B、
| ||
C、
| ||
D、
|
 )时所需要的时间.
)时所需要的时间.