题目内容
如图,抛物线y=ax2-2ax+c的图象与x轴交于A、B(3,0),与y轴交于C(0,-
)
(1)求二次函数解析式;
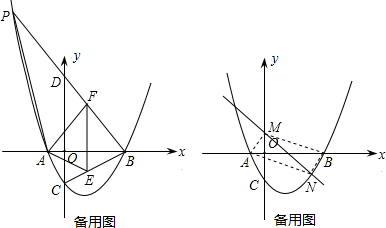
(2)P为第二象限抛物线上一点,且∠PBA=∠OCB,点E在线段CB上,过E作x轴的垂线交PB于F,当△AEF面积最大时,求点E坐标;
(3)设直线l:y=kx+b交y轴于M,交抛物线于N,若A、M、N、B为顶点的四边形为平行四边形,求直线l解析式.

| 3 |
| 2 |
(1)求二次函数解析式;
(2)P为第二象限抛物线上一点,且∠PBA=∠OCB,点E在线段CB上,过E作x轴的垂线交PB于F,当△AEF面积最大时,求点E坐标;
(3)设直线l:y=kx+b交y轴于M,交抛物线于N,若A、M、N、B为顶点的四边形为平行四边形,求直线l解析式.

考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)把点B、C的坐标代入抛物线解析式,利用待定系数法求函数解析式解答;
(2)设PB与y轴相交于点D,根据点B、C的坐标求出OC、OB的长度,然后利用相似三角形对应边成比例求出OD的长度,从而得到点D的坐标,再利用待定系数法求直线解析式求出直线PB的解析式与直线BC的解析式,设点E的横坐标为x,根据两直线的解析式表示出E、F的坐标,再根据抛物线解析式求出点A的坐标,然后表示出EF的长度与点A到EF的距离,然后根据三角形的面积公式列式整理,再根据二次函数的最值问题解答得到x的值,便不难求出点E的坐标;
(3)先根据AB的坐标求出AB的长度,再分①AB是平行四边形的边时,直线l与x轴平行,根据平行四边形对边相等求出MN的长度,然后分点N在第一象限与第二象限得到点N的横坐标,再代入抛物线解析式计算求出纵坐标,从而得解;②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分求出平行四边形的中心坐标是(1,0),然后求出点N的横坐标是2,代入抛物线解析式求出点N的纵坐标,再利用待定系数法求直线解析式计算即可得解.
(2)设PB与y轴相交于点D,根据点B、C的坐标求出OC、OB的长度,然后利用相似三角形对应边成比例求出OD的长度,从而得到点D的坐标,再利用待定系数法求直线解析式求出直线PB的解析式与直线BC的解析式,设点E的横坐标为x,根据两直线的解析式表示出E、F的坐标,再根据抛物线解析式求出点A的坐标,然后表示出EF的长度与点A到EF的距离,然后根据三角形的面积公式列式整理,再根据二次函数的最值问题解答得到x的值,便不难求出点E的坐标;
(3)先根据AB的坐标求出AB的长度,再分①AB是平行四边形的边时,直线l与x轴平行,根据平行四边形对边相等求出MN的长度,然后分点N在第一象限与第二象限得到点N的横坐标,再代入抛物线解析式计算求出纵坐标,从而得解;②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分求出平行四边形的中心坐标是(1,0),然后求出点N的横坐标是2,代入抛物线解析式求出点N的纵坐标,再利用待定系数法求直线解析式计算即可得解.
解答:解:(1)∵抛物线y=ax2-2ax+c的图象经过B(3,0),C(0,-
),
∴
,
解得
,
所以,抛物线解析式为y=
x2-x-
;
(2)如图,设直线PB与y轴相交于点D,
∵B(3,0),C(0,-
),
∴OC=
,OB=3,
∵∠PBA=∠OCB,∠BOC=∠BOD=90°,
∴△BOC∽△DOB,
∴
=
,
即
=
,
解得OD=6,
∴点D的坐标为(0,6),
设直线PB的解析式为y=ex+f,直线BC的解析式为y=mx+n,
则
,
,
解得
,
,
所以,直线PB的解析式为y=-2x+6,直线BC的解析式为y=
x-
,
令y=0,则
x2-x-
=0,
解得x1=3,x2=-1,
所以,点A的坐标为(-1,0),
设点E的横坐标为x,则点E(x,
x-
),F(x,-2x+6),
EF=-2x+6-
x+
=-
x+
,
点A到EF的距离为x-(-1)=x+1,
S△AEF=
×(-
x+
)×(x+1),
=-
(x-3)(x+1),
=-
(x2-2x-3),
=-
(x-1)2+5,
所以,当x=1时,△AEF面积最大,
此时
×1-
=-1,
所以,点E的坐标为(1,-1);
(3)∵A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
①AB是平行四边形的边时,直线l与x轴平行,
此时k=0,MN=AB=4,
所以,点N的横坐标为4或-4,
当点N的横坐标为4时,y=
×42-4-
=
,
此时,直线l的解析式为y=
,
当点N的横坐标为-4时,y=
×(-4)2-(-4)-
=
,
此时,直线l的解析式为y=
,
②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分,
∵A(-1,0),B(3,0),
∴平行四边形的中心坐标为(1,0),
∵点M在y轴上,
∴点N的横坐标为2,
此时,y=
×22-2-
=-
,
∴点N的坐标为(2,-
),
∴
,
解得
,
所以,直线l的解析式为y=-
x+
,
综上所述,直线l的解析式为:y=
或y=
或y=-
x+
.
| 3 |
| 2 |
∴
|
解得
|
所以,抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)如图,设直线PB与y轴相交于点D,
∵B(3,0),C(0,-
| 3 |
| 2 |
∴OC=
| 3 |
| 2 |
∵∠PBA=∠OCB,∠BOC=∠BOD=90°,
∴△BOC∽△DOB,
∴
| OD |
| OB |
| OB |
| OC |
即
| OD |
| 3 |
| 3 | ||
|
解得OD=6,
∴点D的坐标为(0,6),
设直线PB的解析式为y=ex+f,直线BC的解析式为y=mx+n,
则
|
|
解得
|
|

所以,直线PB的解析式为y=-2x+6,直线BC的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
令y=0,则
| 1 |
| 2 |
| 3 |
| 2 |
解得x1=3,x2=-1,
所以,点A的坐标为(-1,0),
设点E的横坐标为x,则点E(x,
| 1 |
| 2 |
| 3 |
| 2 |
EF=-2x+6-
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
点A到EF的距离为x-(-1)=x+1,
S△AEF=
| 1 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
=-
| 5 |
| 4 |
=-
| 5 |
| 4 |
=-
| 5 |
| 4 |
所以,当x=1时,△AEF面积最大,
此时
| 1 |
| 2 |
| 3 |
| 2 |
所以,点E的坐标为(1,-1);
(3)∵A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
①AB是平行四边形的边时,直线l与x轴平行,
此时k=0,MN=AB=4,
所以,点N的横坐标为4或-4,
当点N的横坐标为4时,y=
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
此时,直线l的解析式为y=
| 5 |
| 2 |
当点N的横坐标为-4时,y=
| 1 |
| 2 |
| 3 |
| 2 |
| 21 |
| 2 |
此时,直线l的解析式为y=
| 21 |
| 2 |
②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分,
∵A(-1,0),B(3,0),
∴平行四边形的中心坐标为(1,0),
∵点M在y轴上,
∴点N的横坐标为2,
此时,y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴点N的坐标为(2,-
| 3 |
| 2 |
∴
|
解得
|
所以,直线l的解析式为y=-
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,直线l的解析式为:y=
| 5 |
| 2 |
| 21 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题是对二次函数的综合考查,主要利用了待定系数法求函数解析式,相似三角形对应边成比例,三角形的面积,二次函数的最值问题,平行四边形的对边平行且相等,对角线互相平分的性质,(3)要注意AB为平行四边形的边时,直线l与x轴平行的情况的讨论.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
将点P(4,3)向下平移1个单位后,落在反比例函数y=
的图象上,则k的值为( )
| k |
| x |
| A、12 | B、10 | C、9 | D、8 |
已知
+|3x-2y-a|=0,y为负数,则a的取值范围为( )
| x-2 |
| A、a≥2 | B、a<3 |
| C、a>6 | D、a≥5 |
已知
=
,
=
,
=
,则
=( )
| xy |
| x+y |
| 1 |
| 3 |
| yz |
| y+z |
| 1 |
| 5 |
| zx |
| z+x |
| 1 |
| 6 |
| xyz |
| xy+yz+zx |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是( )
如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是( )| A、50° | B、60° |
| C、70° | D、80° |
 已知二次函数y=ax2+(a2-3a-4)x-12a的图象关于y轴对称,并有最大值.
已知二次函数y=ax2+(a2-3a-4)x-12a的图象关于y轴对称,并有最大值. )时所需要的时间.
)时所需要的时间. 如图,梯形ABCD中,AD∥BC,AB⊥AD,AD=7,BC=9.若DE⊥DC,且DE=DC,则△ADE的面积是
如图,梯形ABCD中,AD∥BC,AB⊥AD,AD=7,BC=9.若DE⊥DC,且DE=DC,则△ADE的面积是