题目内容
6.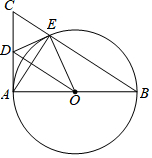 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC交⊙O于点E.(1)若D为AC的中点,证明:DE是⊙O的切线;
(2)若OA=$\sqrt{3}$,CE=1,求∠ACB的度数.
分析 (1)由AB是⊙O的直径,得到∠AEB=90°,根据直角三角形的性质得到AD=DE,求得∠DAE=∠AED,根据切线的性质得到∠CAE+∠EAO=∠CAB=90°,等量代换得到∠DEO=90°,于是得到结论;
(2)根据射影定理得到AB2=BE•BC,求得BE=3,(负值舍去),得到BC=4,根据三角函数的定义即刻得到结论.
解答 解:(1)∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠AEC=90°,
∵D为AC的中点,
∴AD=DE,
∴∠DAE=∠AED,
∵AC是⊙O的切线,
∴∠CAE+∠EAO=∠CAB=90°,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DEA+∠OEA=90°,
∴∠DEO=90°,
∴DE是⊙O的切线;
(2)∵OA=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
∵∠CAB=90°,AE⊥BC,
∴AB2=BE•BC,
即(2$\sqrt{3}$)2=BE(BE+1),
∴BE=3,(负值舍去),
∴BC=4,
∵sin∠ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{2}$,
∴∠ACB=60°.
点评 本题考查了切线的判定和性质,直角三角形的性质,等腰三角形的性质,射影定理,特殊角的三角函数,正确的识别图形是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
1.在平面直角坐标系中,一条直线经过第三象限内A、B两点,过A、B分别作两坐标轴的垂线与两坐标轴围成的矩形周长均为10,则该直线的函数表达式为( )
| A. | y=x-5 | B. | y=x-10 | C. | y=-x-5 | D. | y=-x-10 |
15.实数$\sqrt{2}$-1的相反数是( )
| A. | $\sqrt{2}$+1 | B. | -$\sqrt{2}$+1 | C. | -$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |

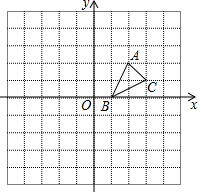 如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).
如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1). 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n),交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n),交y轴于点B,交x轴于点D.