题目内容

1．在平面直角坐标系中，一条直线经过第三象限内A、B两点，过A、B分别作两坐标轴的垂线与两坐标轴围成的矩形周长均为10，则该直线的函数表达式为（　　）
A．y=x-5B．y=x-10C．y=-x-5D．y=-x-10

分析 设A点坐标为（x，y），由坐标的意义可知AC=-x，AD=-y，根据题意可得到x、y之间的关系式，可得出答案．

解答 解：如图，设A点坐标为（x，y），过A点分别作AD⊥x轴，AC⊥y轴，垂足分别为D、C，
∵P点在第三象限，
∴AC=-x，AD=-y，
∵矩形ADOC的周长为10，
∴2（-x-y）=10，
∴x+y=-5，即y=-x-5，
故选C．

点评 本题考查了矩形的性质，一次函数图象上点的坐标特征以及点的坐标的意义，根据坐标的意义得出x、y之间的关系是解题的关键．

练习册系列答案
相关题目
11．已知二次函数y=x2-4x+3．
（1）请直接写出此抛物线的顶点坐标及对称轴；
（2）求出此抛物线与两坐标轴的交点坐标．
12．一元二次方程2x2-8=0的根为x1=2，x2=-2．
9．（1）一个两位数，其中a表示十位上的数字，b表示个位上的数字（a≠b，ab≠0），把十位、个位上的数字互换位置得到一个新两位数．则这两个两位数的和一定能被11整除，这两个两位数的差一定能被9整除．
（2）将一个正整数从个位到最高位的数字依次重新书写成一个新数，恰好与原数相同，我们把这样的正整数称为“对称数”，如：5，33，565，2552，12421分别是一位、两位、三位、四位、五位“对称数”．
①请你写出2个四位“对称数”，猜想任意一个四位“对称数”，能否被11整除，并用字母式子说明理由；
②已知一个能被11整除的三位“对称数”，设其个位上的数字为x（1≤x≤4），十位上的数字为y，求y与x的数量关系，并写出所有能被11整除的三位“对称数”．
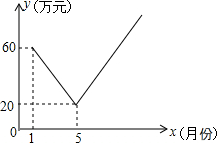16．保护生态环境，实行“节能减排”的理念已深入人心．我市某工厂从2016年1月开始，进行机器设备更新，产业转型换代的改造，改造期间利润明显下降，从1月利润60万元逐月等额下降，到5月份利润为20万元．5月底改造完成，从这时起，该厂每个月的利润都比上个月增加15万元．设第x个月的利润为y（万元），函数图象如图．
（1）分别求出改造期间与改造完成后y与x的函数关系式．
（2）该厂几月份的利润为50万元？
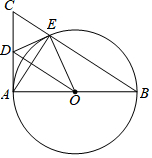6．如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC交⊙O于点E．
（1）若D为AC的中点，证明：DE是⊙O的切线；
（2）若OA=$\sqrt{3}$，CE=1，求∠ACB的度数．
13．如图，菱形ABCD中，∠ABD=65°，则∠A=50°．
10．下列图形中，既是中心对称图形又是轴对称图形的个数是（　　）
A．4个B．3个C．2个D．1个
10．计算：
（1）$\frac{{{a^2}x}}{{b{y^2}}}$•$\frac{{a{y^2}}}{{{b^2}x}}$；                
（2）$\frac{x-2}{x+3}$•$\frac{{{x^2}-9}}{{{x^2}-4}}$；
（3）（$\frac{-3ac}{2b}$）2÷（-9ac2）；          
（4）$\frac{{{{（{a-b}）}^2}}}{ab}$-$\frac{{{a^2}-{b^2}}}{ab}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网