题目内容
8.在△ABC中,|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,则∠A=105°.分析 利用偶次方的性质以及绝对值的性质得出∠C=45°,∠B=30°,进而得出答案.
解答 解:∵|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,
∴sinC-$\frac{\sqrt{2}}{2}$=0,$\frac{\sqrt{3}}{2}$-cosB=0,
∴∠C=45°,∠B=30°,
∴∠A=180°-45°-30°=105°.
故答案为:105°.
点评 此题主要考查了特殊角的三角函数值以及绝对值和偶次方的性质,正确记忆特殊角的三角函数值是解题关键.

练习册系列答案
相关题目
19.“十、一”黄金周期间,阜阳生态园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)若9月30日的游客人数为5千人,门票每人10元.问黄金周期间阜阳生态园门票收入是多少元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:千人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)若9月30日的游客人数为5千人,门票每人10元.问黄金周期间阜阳生态园门票收入是多少元?
13.在下列各式中属于分式的是( )
| A. | $\frac{3x}{π}$ | B. | $\frac{x-y}{4}$ | C. | $\frac{x+y}{x-y}$ | D. | 3x+$\frac{1}{2}$ |
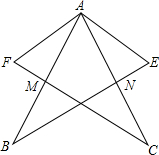 如图,AB=AC,AF=AE,AB,FC相交于点M,AC、BE相交于点N,∠FAB=∠EAC.试证明△AFM≌△AEN.
如图,AB=AC,AF=AE,AB,FC相交于点M,AC、BE相交于点N,∠FAB=∠EAC.试证明△AFM≌△AEN. 如图,过正方形ABCD的顶点A作直线l,过点B、D作l的垂线,垂足分别为E、F.若BE=8,DF=6,则AB的长度等于10.
如图,过正方形ABCD的顶点A作直线l,过点B、D作l的垂线,垂足分别为E、F.若BE=8,DF=6,则AB的长度等于10.