题目内容
17. 如图,过正方形ABCD的顶点A作直线l,过点B、D作l的垂线,垂足分别为E、F.若BE=8,DF=6,则AB的长度等于10.
如图,过正方形ABCD的顶点A作直线l,过点B、D作l的垂线,垂足分别为E、F.若BE=8,DF=6,则AB的长度等于10.
分析 先利用AAS判定△ABE≌△ADF,从而得出AE=DF,BE=DF,最后根据勾股定理得出AB的长.
解答 解:如图,∵四边形ABCD是正方形,
∴∠BAE+∠DAF=90°,∠ABF+∠BAE=90°,
∴∠ABE=∠DAF.
在△ABE与△ADF中,$\left\{\begin{array}{l}{∠AEB=∠AFD}\\{∠ABE=∠DAF}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF(AAS),
∴AE=DF,BE=AF,
∴在直角△ABE中,由勾股定理得到:$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{D{F}^{2}+B{E}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
故答案为:10.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ABE≌△ADF是解题的关键.

练习册系列答案
相关题目
7.下列命题正确的是( )
| A. | 一个数的平方大于9,这个数一定大于3 | |
| B. | a,b为有理数,若$\frac{a}{b}$>0,则a>0且b>0 | |
| C. | 设a为一个有理数,则a>$\frac{1}{a}$ | |
| D. | a,b为有理数,若ab=0,则a,b至少有一个为0 |
6.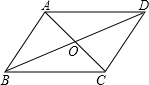 如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
 如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )| A. | 7.5 | B. | 6 | C. | 12 | D. | 10 |
7.以下各式中计算正确的是( )
| A. | -$\sqrt{(-6)^{2}}$=-6 | B. | (-$\sqrt{3}$)2=-3 | C. | $\sqrt{(-16)^{2}}$=±16 | D. | $\sqrt{{a}^{2}}$=a |