题目内容
15.已知函数y=|x2-2x-3|(1)在指定的平面直角坐标系中作出y=|x2-2x-3|的图象;
(2)结合所做出的图象指出x在什么范围内,y随着x增大而增大;
(3)结合所做出的图象,解不等式|x2-2x-3|>5.
分析 (1)首先求得函数与x轴的交点坐标,与y轴的交点坐标,以及对称轴,作出图象即可;
(2)根据图象和对称轴得出y随着x增大而增大对应的x的取值范围;
(3)观察图象得出不等式的解集即可.
解答 解:(1)∵y=|x2-2x-3|=|(x-3)(x+1)|
∴图象与x轴的交点为(-1,0),(3,0),对称轴x=1,与y轴的交点为3,
图象如下:
(2)由图象可知,当-1<x<1,x>3时,y随着x增大而增大;
(3)由x2-2x-3=5,解得x=-2或x=4,
因此当x<-2或x>4时,|x2-2x-3|>5.
点评 此题考查二次函数的性质,二次函数的图象以及二次函数与不等式的关系,求得函数与x轴的交点坐标,与y轴的交点坐标,以及对称轴是解决问题的关键.

练习册系列答案
相关题目
10.已知2是方程x2-ax+2=0的一个根,则方程的另一个根为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
 如图,A、P、B、C四点都在⊙O上,且∠1=∠2=60°,判断△ABC的形状并证明你的结论.
如图,A、P、B、C四点都在⊙O上,且∠1=∠2=60°,判断△ABC的形状并证明你的结论. 已知:如图,在△ABC中,AC=2.BC=3.∠C=60°. 求△ABC外接圆⊙O的半径r.
已知:如图,在△ABC中,AC=2.BC=3.∠C=60°. 求△ABC外接圆⊙O的半径r.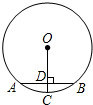 如图,AB为⊙O的弦,⊙O的半径为13,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是10.
如图,AB为⊙O的弦,⊙O的半径为13,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是10.