题目内容
4.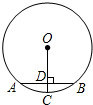 如图,AB为⊙O的弦,⊙O的半径为13,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是10.
如图,AB为⊙O的弦,⊙O的半径为13,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是10.
分析 连接OA,根据垂径定理求出AB=2AD,求出OA、OD,根据勾股定理求出AD即可.
解答 解:
连接OA,
∵OC⊥AB,OC过O,
∴AB=2AD,∠ADO=90°,
∵CD=1,⊙O的半径为13,
∴OD=12,OA=13,
在Rt△ADO中,由勾股定理得:AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴AB=10,
故答案为:10.
点评 本题考查了勾股定理,垂径定理的应用,能求出AB=2AD和AD的长是解此题的关键,注意:垂直于弦的直径平分这条弦.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
13.下列实数是无理数的是( )
| A. | -1 | B. | $\sqrt{9}$ | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
 如图,在梯形ABCD中,CD∥AB,BE是∠ABC的平分线,BE⊥AD于E,且$\frac{DE}{AE}$=$\frac{1}{2}$,求$\frac{{S}_{△ABE}}{{S}_{四边形BCDE}}$的值.
如图,在梯形ABCD中,CD∥AB,BE是∠ABC的平分线,BE⊥AD于E,且$\frac{DE}{AE}$=$\frac{1}{2}$,求$\frac{{S}_{△ABE}}{{S}_{四边形BCDE}}$的值. 在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?
在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?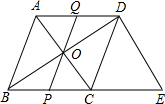 在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6,过D点作DE∥AC交BC的延长线于点E.
在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6,过D点作DE∥AC交BC的延长线于点E. 如图所示,在等腰梯形ABCD中,AB∥CD,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积是18cm2.
如图所示,在等腰梯形ABCD中,AB∥CD,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积是18cm2. 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).