题目内容
3.若一个多边形的内角由小到大依次相差10°,则此多边形的边数可能是多少?分析 设最小角为a度,边长为n,则内角和为(n-2)•180°,n个内角分别为a,a+10°,a+20°,…,a+(n-1)10°,所以a+a+10+a+20+…+a+(n-1)10=(n-2)•180,整理可得:na+5n2-5n=180n-360,解得:a=$\frac{-5{n}^{2}+185n-360}{n}$,即可解答.
解答 解:设最小角为a度,边长为n,
则内角和为(n-2)•180°,n个内角分别为a,a+10°,a+20°,…,a+(n-1)10°,
∴a+a+10+a+20+…+a+(n-1)10=(n-2)•180,
∴na+$\frac{n(n-1)}{2}$×10=180(n-2),
∴na+5n2-5n=180n-360,
解得:a=$\frac{-5{n}^{2}+185n-360}{n}$,
∴n=3(50°,60° 70°)
n=4(75°,85°,95°,105°)
n=5(88°,98°,108°,118°,128°)
n=6(95°,105°,115°,125°,135°,145°)
n=8(100°,110°,120°,130°,140°,150°,160°,170°).
点评 本题考查了多边形的内角与外角,解决本题的关键是熟记多边形的内角和.

练习册系列答案
相关题目
10. 如图,在平面直角坐标系中,△ABC的面积是( )
如图,在平面直角坐标系中,△ABC的面积是( )
 如图,在平面直角坐标系中,△ABC的面积是( )
如图,在平面直角坐标系中,△ABC的面积是( )| A. | 2 | B. | 4 | C. | 8 | D. | 6 |
13.下列实数是无理数的是( )
| A. | -1 | B. | $\sqrt{9}$ | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
 如图,在梯形ABCD中,CD∥AB,BE是∠ABC的平分线,BE⊥AD于E,且$\frac{DE}{AE}$=$\frac{1}{2}$,求$\frac{{S}_{△ABE}}{{S}_{四边形BCDE}}$的值.
如图,在梯形ABCD中,CD∥AB,BE是∠ABC的平分线,BE⊥AD于E,且$\frac{DE}{AE}$=$\frac{1}{2}$,求$\frac{{S}_{△ABE}}{{S}_{四边形BCDE}}$的值.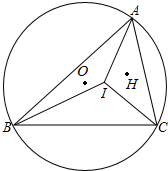 锐角△ABC中,AB>BC>CA,O、I、H分别是它的外心、内心,垂心,已知∠A=60°,求证:(1)∠OIH-∠ABC是一个定值;(2)∠OIH+∠ACB也是一个定值.
锐角△ABC中,AB>BC>CA,O、I、H分别是它的外心、内心,垂心,已知∠A=60°,求证:(1)∠OIH-∠ABC是一个定值;(2)∠OIH+∠ACB也是一个定值. 在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?
在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?