题目内容
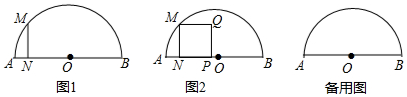
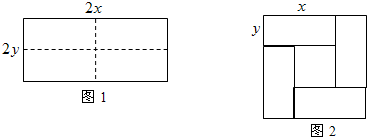
18.如图1,半圆O的半径r=5cm,点N是半径AO上的一个动点,N从点A出发,沿AO方向以1cm/s的速度向点O运动,过点N作MN⊥AB,交半圆O于点M,设运动时间为ts.(1)当t等于多少时,MN=3cm?
(2)如图2,以MN为边在半圆O内部作正方形MNPQ,使得点P落在AB上,点Q落在半圆内(或半圆上),设正方形MNPQ的面积为S,求S与t之间的函数关系式以及自变量t的取值范围.
分析 (1)如图1,连接OM,由题意得AN=t、ON=5-t,由勾股定理知MN=$\sqrt{O{M}^{2}-O{N}^{2}}$=$\sqrt{{5}^{2}-(5-t)^{2}}$=$\sqrt{-{t}^{2}+10t}$,根据MN=3可得关于t的方程,解之可得;
(2)由S=MN2可得函数解析式,如图2,连接OM、OQ,证Rt△OMN≌Rt△OQP得ON=OP=$\frac{1}{2}$NP=$\frac{1}{2}$MN,即2ON=MN,从而得出关于t的方程,解之可得t的最大值,即可确定t的取值范围.
解答 解:(1)如图1,连接OM,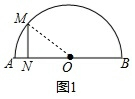
由题意知AN=t,
则ON=5-t,
∴MN=$\sqrt{O{M}^{2}-O{N}^{2}}$=$\sqrt{{5}^{2}-(5-t)^{2}}$=$\sqrt{-{t}^{2}+10t}$,
当MN=3时,得$\sqrt{-{t}^{2}+10t}$=3,
解得:t=1或t=9,
又t≤5,
∴t=1,
答:当t等于1时,MN=3cm;
(2)由(1)知,MN=$\sqrt{-{t}^{2}+10t}$,
∴S=MN2=-t2+10t,
如图2,连接OM、OQ,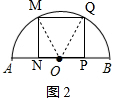
则OM=OQ,
在Rt△OMN和Rt△OQP中,
∵$\left\{\begin{array}{l}{MN=QP}\\{OM=OQ}\end{array}\right.$,
∴Rt△OMN≌Rt△OQP,
∴ON=OP=$\frac{1}{2}$NP=$\frac{1}{2}$MN,即2ON=MN,
∴2(5-t)=$\sqrt{-{t}^{2}+10t}$,
解得:x=5+$\sqrt{5}$>5(舍)或x=5-$\sqrt{5}$,
又∵x≥0,
∴0≤x≤5-$\sqrt{5}$,
故S=-t2+10t,(0≤x≤5-$\sqrt{5}$).
点评 本题主要考查二次函数的应用、勾股定理、全等三角形的判定与性质,熟练掌握勾股定理、全等三角形的判定与性质及正方形的性质是解题的关键.

 名校课堂系列答案
名校课堂系列答案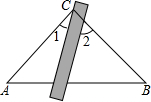 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )| A. | 33° | B. | 23° | C. | 67° | D. | 无法确定 |
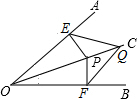 已知OC平分∠AOB,点P,Q都是OC上不同的点,PE⊥OA,PF⊥OB,连接EQ,FQ,求证:FQ=EQ.
已知OC平分∠AOB,点P,Q都是OC上不同的点,PE⊥OA,PF⊥OB,连接EQ,FQ,求证:FQ=EQ.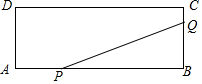 如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).