题目内容
7.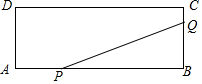 如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
分析 (1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.
解答 解:(1)∵S△PBQ=$\frac{1}{2}$PB•BQ,PB=AB-AP=18-2x,BQ=x,
∴y=$\frac{1}{2}$ (18-2x)x,
即y=-x2+9x(0<x≤4);
(2)由(1)知,y=-x2+9x,
∴y=-$(x-\frac{9}{2})^{2}+\frac{81}{4}$,
∵当0<x≤$\frac{9}{2}$时,y随x的增大而增大,
而0<x≤4,
∴当x=4时,y最大值=20,
即△PBQ的最大面积是20 cm2.
点评 本题考查了矩形的性质,二次函数的最值问题,根据题意表示出PB、BQ的长度是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
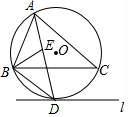 如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.
如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC. 如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.