题目内容
10.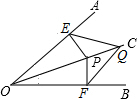 已知OC平分∠AOB,点P,Q都是OC上不同的点,PE⊥OA,PF⊥OB,连接EQ,FQ,求证:FQ=EQ.
已知OC平分∠AOB,点P,Q都是OC上不同的点,PE⊥OA,PF⊥OB,连接EQ,FQ,求证:FQ=EQ.
分析 根据角平分线的性质得到PE=PF,得到Rt△EOP≌Rt△FOP,根据线段垂直平分线的判定和性质证明.
解答 证明:∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF,
在Rt△EOP和Rt△FOP中,
$\left\{\begin{array}{l}{OP=OP}\\{PE=PF}\end{array}\right.$,
∴Rt△EOP≌Rt△FOP,
∴OE=OF,
∴OC是线段EF的垂直平分线,
∴FQ=EQ.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
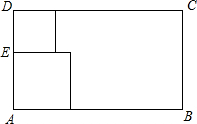 如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?
如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?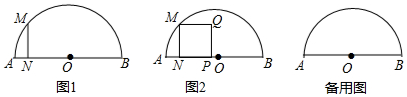
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,如果AD=5,BD=20,求CD、AC的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,如果AD=5,BD=20,求CD、AC的长.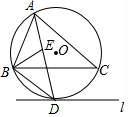 如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.
如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC. 如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π. 已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为2 cm.
已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为2 cm.