题目内容
11.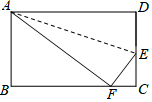 如图,在长方形ABCD中,DC=9.在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.
如图,在长方形ABCD中,DC=9.在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.
分析 根据三角形的面积求出BF,利用勾股定理列式求出AF,再根据翻折变换的性质可得AD=AF,然后求出CF,设DE=x,表示出EF、EC,然后在Rt△CEF中,利用勾股定理列方程求解即可.
解答 解:在长方形ABCD中,DC=9,
所以,AB=DC=9,
∵△ABF的面积为54,
∴$\frac{1}{2}$×9•BF=54,
解得BF=12,
由勾股定理得,AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∵△AED沿AE折叠点D落在BC上点F处,
∴AD=AF=15,DE=EF,
∴CF=BC-BF=15-12=3,
设DE=x,则EF=x,EC=9-x,
在Rt△CEF中,由勾股定理得,CF2+EC2=EF2,
即32+(9-x)2=x2,
解得x=5,
∴DE=5.
点评 本题考查了翻折变换的性质,矩形的性质,三角形的面积,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
6.下列说法中,不正确的是( )
| A. | 三边长度之比为5:12:13的三角形是直角三角形 | |
| B. | 三个角的度数之比为1:3:4的三角形是直角三角形 | |
| C. | 三个角的度数之比为3:4:5的三角形是直角三角形 | |
| D. | 三边长度之比为$\sqrt{3}$:2:$\sqrt{7}$的三角形是直角三角形 |
16.已知P(x,y)在第二象限,且x2=4,|y|=7,则点P的坐标是( )
| A. | (2,-7) | B. | (-4,7) | C. | (4,-7) | D. | (-2,7) |
2.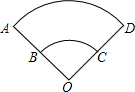 如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )
如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )
 如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )
如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )| A. | 2倍 | B. | 4倍 | C. | $\frac{1}{2}$倍 | D. | $\frac{1}{4}$倍 |
3.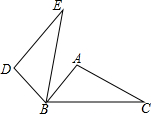 如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
 如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )| A. | 50° | B. | 70° | C. | 80° | D. | 90° |
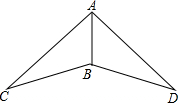 如图,△ABC与△ABD中,BC=BD,AE、AF分别是∠BAC、∠BAD的角平分线.
如图,△ABC与△ABD中,BC=BD,AE、AF分别是∠BAC、∠BAD的角平分线.