题目内容
1.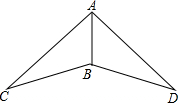 如图,△ABC与△ABD中,BC=BD,AE、AF分别是∠BAC、∠BAD的角平分线.
如图,△ABC与△ABD中,BC=BD,AE、AF分别是∠BAC、∠BAD的角平分线.(1)请你在原图中作出两个三角形的角平分线AE和AF (要求用尺规作图,保留作图痕迹,不写作法与证明);
(2)若∠ABC=∠ABD,请你证明△ABE≌△ABF.
分析 (1)分别作出∠CAB、∠BAD的角平分线即可;
(2)首先证明△ABC≌△ABD,推出∠CAB=∠DAB,由∠EAB=$\frac{1}{2}$∠CAB,∠BAF=$\frac{1}{2}$∠BAD,可知∠BAE=∠BAF,推出△ABE≌△ABF即可解决问题.
解答 解:(1)如图所示,线段AE、AF即为所求.
(2)在△ABC和△ABD中,
$\left\{\begin{array}{l}{AB=AB}\\{∠ABC=∠ABD}\\{BC=BD}\end{array}\right.$,
∴△ABC≌△ABD,
∴∠CAB=∠DAB,
∵∠EAB=$\frac{1}{2}$∠CAB,∠BAF=$\frac{1}{2}$∠BAD,
∴∠BAE=∠BAF,
在△ABE和△ABF中,
$\left\{\begin{array}{l}{∠EAB=∠FAB}\\{AB=AB}\\{∠ABE=∠ABF}\end{array}\right.$,
∴△ABE≌△ABF.
点评 本题考查全等三角形的判定和性质、基本作图、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
11. 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )
 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )| A. | 6 | B. | 4 | C. | 64 | D. | 8 |
16.x为任意实数时,下列分式一定有意义的是( )
| A. | $\frac{x+5}{{x}^{2}}$ | B. | $\frac{x-1}{{x}^{3}+1}$ | C. | $\frac{x+1}{{x}^{2}-9}$ | D. | $\frac{x+1}{|x|+1}$ |
6.下列四个函数:①y=-2x+1,②y=3x-2,③y=-$\frac{3}{x}$,④y=x2+2,当x>0时,y随x的增大而增大的函数是( )
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ②④ |
10.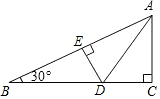 如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )
如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )
 如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )
如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )| A. | 19.5cm | B. | 20cm | C. | 20.5cm | D. | 19cm |
 如图,已知△ABC,AB=AC,∠A=36°
如图,已知△ABC,AB=AC,∠A=36°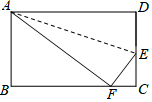 如图,在长方形ABCD中,DC=9.在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.
如图,在长方形ABCD中,DC=9.在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.