题目内容
3.在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为($\frac{{{x_1}+{x_2}}}{2}$,$\frac{{{y_1}+{y_2}}}{2}}$).现有A(3,4),B(1,8),C(-2,6)三点,点D为线段AB的中点,点C为线段AE的中点,则线段DE的中点坐标为(-$\frac{5}{2}$,7).分析 根据线段的中点坐标公式先求出点D与点E的坐标,再求出线段DE的中点坐标即可.
解答 解:∵点D为线段AB的中点,A(3,4),B(1,8),
∴D(2,6).
∵点C为线段AE的中点,A(3,4),C(-2,6),
∴E(-7,8),
∴线段DE的中点坐标为(-$\frac{5}{2}$,7).
故答案为(-$\frac{5}{2}$,7).
点评 本题考查了坐标与图形性质,掌握以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为($\frac{{{x_1}+{x_2}}}{2}$,$\frac{{{y_1}+{y_2}}}{2}}$)并能灵活应用是解题的关键..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.甲、乙两人骑自行车比赛,若甲先骑30分钟,则乙出发后50分钟可追上甲,设甲、乙每小时分别骑x千米、y千米,则可列方程( )
| A. | 30x=50y | B. | $\frac{1}{2}x=({\frac{1}{2}+\frac{5}{6}})y$ | C. | (30+50)x=50y | D. | $({\frac{1}{2}+\frac{5}{6}})x=\frac{5}{6}y$ |
15.下列关系式正确的是( )
| A. | (2a+1)2=2a2+1 | B. | (2a-1)2=4a2-1 | ||
| C. | (3a+2b)(3a-2b)=9a2-4b2 | D. | (2a-1)2=4a2+4a+1 |
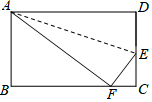 如图,在长方形ABCD中,DC=9.在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.
如图,在长方形ABCD中,DC=9.在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.