题目内容
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
考点:抛物线与x轴的交点
专题:
分析:根据抛物线的性质得到B(-2,0),C(2,0),A(0,-4),利用两点间的距离公式可以求得△ABC的三边长度,利用三角形的周长公式进行解答.
解答:解:∵抛物线y=x2-4与x轴交于B、C两点,顶点为A,
∴B(-2,0),C(2,0),A(0,-4).
∴AB=4,BC=AC=
=2
,
∴△ABC周长为:AB+BC+AC=4+4
.
故应选B.
∴B(-2,0),C(2,0),A(0,-4).
∴AB=4,BC=AC=
| 22+42 |
| 5 |
∴△ABC周长为:AB+BC+AC=4+4
| 5 |
故应选B.
点评:本题考查的是二次函数和x轴的交点问题,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
 如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与与y轴交与点H,点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),且∠OEF=∠A=∠DOC,CD=10,sin∠OCD=
如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与与y轴交与点H,点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),且∠OEF=∠A=∠DOC,CD=10,sin∠OCD=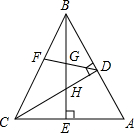 在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.
在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2. 如图所示,CE⊥AB,BD⊥AC,BF=CF,求证:AF为∠BAC的平分线.
如图所示,CE⊥AB,BD⊥AC,BF=CF,求证:AF为∠BAC的平分线. 如图,⊙O的直径AB=4,半径OC⊥AB,D为弧BC上一点,DE⊥OC,DF⊥AB,垂足分别为E、F.则EF=
如图,⊙O的直径AB=4,半径OC⊥AB,D为弧BC上一点,DE⊥OC,DF⊥AB,垂足分别为E、F.则EF=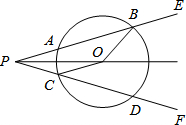 已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和∠EPF的两边分别交于点A、B和C、D.试探究∠OBA与∠OCD的关系,并说明理由.
已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和∠EPF的两边分别交于点A、B和C、D.试探究∠OBA与∠OCD的关系,并说明理由. 已知:AB=CD,AB∥DC,求证:△ABC≌△CDA.
已知:AB=CD,AB∥DC,求证:△ABC≌△CDA.