题目内容
 已知:AB=CD,AB∥DC,求证:△ABC≌△CDA.
已知:AB=CD,AB∥DC,求证:△ABC≌△CDA.考点:全等三角形的判定
专题:证明题
分析:由平行可得∠1=∠2,加上AB=CD,且AC为公共边可证得结论.
解答:证明:∵AB∥CD,
∴∠1=∠2,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SAS).
∴∠1=∠2,
在△ABC和△CDA中,
|
∴△ABC≌△CDA(SAS).
点评:本题主要考查三角形全等的判定,正确掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
下列函数中,反比例函数是( )
| A、y=x-1 | ||
B、y=
| ||
C、y=
| ||
D、y=
|
下列说法错误的是( )
| A、矩形的对角线互相平分 |
| B、矩形的对角线相等 |
| C、有一个角是直角的四边形是矩形 |
| D、有一个角是直角的平行四边形叫做矩形 |
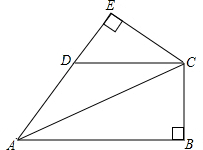 已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.
已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.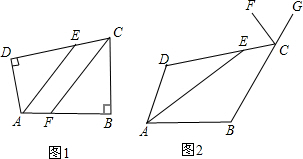 在四边形ABCD中,∠B=∠D=α.
在四边形ABCD中,∠B=∠D=α. 如图,∠1=∠2,BC=EF,需要添加一个条件,才能使△ABC≌△DEF,你添加的条件是
如图,∠1=∠2,BC=EF,需要添加一个条件,才能使△ABC≌△DEF,你添加的条件是