题目内容
已知:
=
=
,求
的值.
| 2a-b-c |
| a |
| -a-c+2b |
| b |
| -a-b+2c |
| c |
| (a+c)(b+c)(a+b) |
| abc |
考点:比例的性质
专题:
分析:设比值为k,表示出b+c、a+c、a+b,再利用等比性质求出k值,然后代入比例式进行计算即可得解.
解答:解:设比值为k,则2a-b-c=ka,
-a-c+2b=kb,
-a-b+2c=kc,
所以,b+c=(2-k)a,
a+c=(2-k)b,
a+b=(2-k)c,
∵
=
=
,
∴
=k=0,
∴
=
=(2-k)3,
∵k=0,
∴(2-k)3=(2-0)3=8,
∴
=8.
-a-c+2b=kb,
-a-b+2c=kc,
所以,b+c=(2-k)a,
a+c=(2-k)b,
a+b=(2-k)c,
∵
| 2a-b-c |
| a |
| -a-c+2b |
| b |
| -a-b+2c |
| c |
∴
| 2a-b-c-a-c+2b-a-b+2c |
| a+b+c |
∴
| (a+c)(b+c)(a+b) |
| abc |
| (2-k)b•(2-k)a•(2-k)c |
| abc |
∵k=0,
∴(2-k)3=(2-0)3=8,
∴
| (a+c)(b+c)(a+b) |
| abc |
点评:本题考查了比例的性质,主要利用了等比性质,利用“设k法”求解并求出k值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
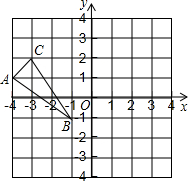 如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).
如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).