题目内容
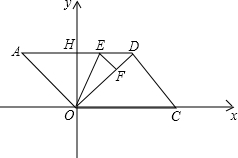
 如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与与y轴交与点H,点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),且∠OEF=∠A=∠DOC,CD=10,sin∠OCD=
如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与与y轴交与点H,点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),且∠OEF=∠A=∠DOC,CD=10,sin∠OCD=| 4 |
| 5 |
(1)求点C、D的坐标;
(2)设AE=x,OF=y,求y关于x的函数关系式,并写出x的取值范围;
(3)点E在边AD上移动的过程中,△OEF是否有可能成为一个等腰三角形?若有可能,请求出x的值;若不可能,请说明理由.
考点:一次函数综合题
专题:
分析:(1)因为四边形AOCD是平行四边形,根据题意求出sin∠OCD=sin∠OAH的值.然后根据勾股定理求出AH的值.又因为∠A=∠DOC,AD∥OC,可推出AH=HD,AD=OC.进而求出C,D的坐标;
(2)已知OA=OD,AE=x,OF=y,可求出FD,AE和DE的表达式之后推出△AEO∽△DFE根据线段的相似比求出y关于x的函数关系式,并写出x的取值范围即;
(3)当点E在边AD上移动的过程中,△OEF可成为一个等腰三角形,根据题意要分为两种情况解答.当OF=EF,求得EO=ED,故可得出(x-6)2+64=(12-x)2求出x的值;当OE=EF时,即
=
=1,易求x的值.
(2)已知OA=OD,AE=x,OF=y,可求出FD,AE和DE的表达式之后推出△AEO∽△DFE根据线段的相似比求出y关于x的函数关系式,并写出x的取值范围即;
(3)当点E在边AD上移动的过程中,△OEF可成为一个等腰三角形,根据题意要分为两种情况解答.当OF=EF,求得EO=ED,故可得出(x-6)2+64=(12-x)2求出x的值;当OE=EF时,即
| AO |
| DE |
| OE |
| EF |
解答:解:(1)∵四边形AOCD是平行四边形,
∴AO=DC=10,∠A=∠OCD,
∴sin∠OCD=sin∠OAH=
,
∴OH=OA•sin∠A=10×
=8,
∴AH=
=6,
又∵∠A=∠DOC,AD∥OC,
∴∠DOC=∠ADO,
∴∠A=∠ADO,OH⊥AD,
∴AH=HD=6,
∴AD=OC=12,
∴D(6,8)、C(12,O);
(2)∵OA=OD=10,
∵OF=x,
∴FD=10-x,AE=t,DE=12-x,
又∵∠OEF=∠EDF,
∴∠AEO+∠FED=180°-∠OEF,∠DEF+∠EFD=180°-∠EDF,
∴∠AEO=∠EFD,∠A=∠EDF,
∴△AEO∽△DFE,
∴
=
,
∴
=
,
即100-10y=12x-x2,
∴y=
x2-
x+10(0<x<12);
(3)当点E在边AD上移动的过程中,△OEF成为一个等腰三角形,
理由如下:
∵∠OFE>∠FDE=∠OEF.
∴OF≠OE.
∴△OEF是等腰三角形,则只有①OF=EF②OE=EF
①当OF=EF时,
∴∠OEF=∠EOF=∠EDO,∴EO=ED.即(x-6)2+64=(12-x)2,x=
;
②当OE=EF时,
则
=
=1即OA=DE.12-x=10,x=2;
∴当x
=或x=2时△OEF是等腰三角形.
∴AO=DC=10,∠A=∠OCD,
∴sin∠OCD=sin∠OAH=
| 4 |
| 5 |
∴OH=OA•sin∠A=10×
| 4 |
| 5 |
∴AH=
| OA2-OH2 |
又∵∠A=∠DOC,AD∥OC,
∴∠DOC=∠ADO,
∴∠A=∠ADO,OH⊥AD,
∴AH=HD=6,
∴AD=OC=12,
∴D(6,8)、C(12,O);

(2)∵OA=OD=10,
∵OF=x,
∴FD=10-x,AE=t,DE=12-x,
又∵∠OEF=∠EDF,
∴∠AEO+∠FED=180°-∠OEF,∠DEF+∠EFD=180°-∠EDF,
∴∠AEO=∠EFD,∠A=∠EDF,
∴△AEO∽△DFE,
∴
| AE |
| DF |
| AO |
| DE |
∴
| x |
| 10-x |
| 10 |
| 12-x |
即100-10y=12x-x2,
∴y=
| 1 |
| 10 |
| 6 |
| 5 |
(3)当点E在边AD上移动的过程中,△OEF成为一个等腰三角形,
理由如下:
∵∠OFE>∠FDE=∠OEF.
∴OF≠OE.
∴△OEF是等腰三角形,则只有①OF=EF②OE=EF
①当OF=EF时,
∴∠OEF=∠EOF=∠EDO,∴EO=ED.即(x-6)2+64=(12-x)2,x=
| 11 |
| 3 |
②当OE=EF时,
则
| AO |
| DE |
| OE |
| EF |
∴当x
| 11 |
| 3 |
点评:本题考查了一次函数综合的知识,用到的知识点主要有勾股定理、相似三角形的判定和性质、等腰三角形的判定和性质、平行四边形的性质,本题是也是函数与几何图形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题,题目的难度较大.

练习册系列答案
相关题目
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
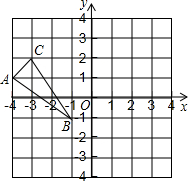 如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).
如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2). 已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.
已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.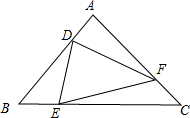 等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形.
等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形. 已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?
已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?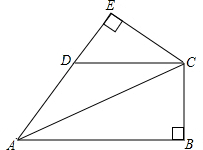 已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.
已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.