题目内容
3.(1)如图①,如果∠B+∠E+∠D=360°,那么AB、CD有怎样的关系,为什么?(2)如图②,当∠1、∠2、∠3满条件∠1+∠3=∠2时,有AB∥CD,为什么?
(3)如图③,当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD,为什么?
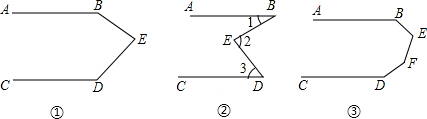
分析 (1)过点E作EF∥AB.由两直线平行,同旁内角互补及已知条件∠B+∠E+∠D=360°求得∠FED+∠EDC=180°;然后根据平行线的传递性证得AB∥CD;
(2)过点E作EF∥AB.由两直线平行,内错角相等求得∠1=∠BEF;再用已知条件∠1+∠3=∠2,∠2=∠BEF+∠DEF推知内错角∠3=∠DEF,所以EF∥CD;最后根据平行线的传递性得出结论;
(3)过点E、F分别作GE∥HF∥CD.根据同旁内角互补以及已知条件求得同旁内角∠ABE+∠BEG=180°,所以AB∥GE;最后根据平行线的传递性来证得AB∥CD.
解答 解:(1)过点E作EF∥AB,如图①,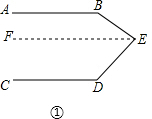
则∠ABE+∠BEF=180°,(两直线平行,同旁内角互补)
因为∠ABE+∠BED+∠EDC=360°,(已知 )
所以∠FED+∠EDC=180°,(等式的性质)
所以 FE∥CD,(同旁内角互补,两直线平行)
∴AB∥CD (或平行线的传递性 ).
(2)如图②,当∠1、∠2、∠3满足条件∠1+∠3=∠2时,有AB∥CD.
理由: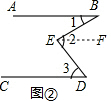
过点E作EF∥AB.
∴∠1=∠BEF;
∵∠1+∠3=∠2,∠2=∠BEF+∠DEF,
∴∠3=∠DEF,
∴EF∥CD,
∴AB∥CD(平行线的传递性);
(3)如图③,当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由: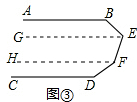
过点E、F分别作GE∥HF∥CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠E+∠F+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
故答案是:(2)∠1+∠3=∠2;
(3)∠B+∠E+∠F+∠D=540°.
点评 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | 2<x<6 | B. | 3<x<9 | C. | 1<x<9 | D. | 2<x<8 |
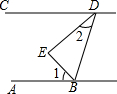 如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由. 如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.
如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.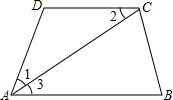 如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.
如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.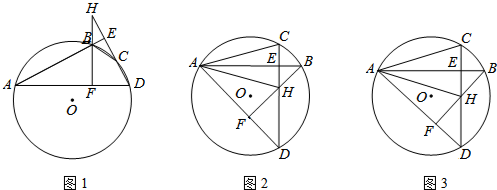
 如图,CD是∠ACB的平分线,∠EDC=25°,∠A=60°,∠B=70°,
如图,CD是∠ACB的平分线,∠EDC=25°,∠A=60°,∠B=70°,