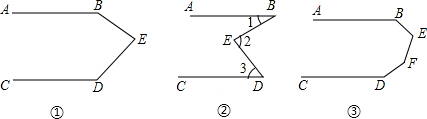题目内容
14. 如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.
如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.
分析 由平行四边形的性质可知“AB∥CE,AD∥BC,AB=CD,AD=BC”,由平行线的性质可得出“∠DAF=∠BCE,∠MCF=∠NAE”,根据全等三角形的判定定理即可得出△ADF≌△CBE,由全等三角形的性质得出AF=CE,再根据边角关系可判定△ANE≌△CMF,由此找出∠MFC=∠NEA,即得出FM∥EN;再由直角三角形的中线等于斜边的一半可得出FM=EN,满足“一组对边平行且相等”,由此证出四边形EMFN是平行四边形.
解答 证明:∵四边形ABCD为平行四边形,
∴AB∥CE,AD∥BC,AB=CD,AD=BC,
∴∠DAF=∠BCE,∠MCF=∠NAE.
∵BE⊥AC于点E,DF⊥AC于点F,
∴∠DFA=∠BEC=∠DFC=∠BEA=90°.
在△ADF和△CBE中,
$\left\{\begin{array}{l}{∠DAF=∠BCE}\\{∠DFA=∠BEC}\\{AD=BC}\end{array}\right.$,
∴△ADF≌△CBE(AAS),
∴AF=CE,
∴AE=AF+EF=CE+EF=CE.
∵M、N分别是DC、AB的中点,
∴AN=CM,
在△ANE和△CMF中,
$\left\{\begin{array}{l}{AN=CM}\\{∠MCF=∠NAE}\\{AE=CF}\end{array}\right.$,
∴△ANE≌△CMF(SAS),
∴∠MFC=∠NEA,
∴FM∥EN.
∵∠DFC=∠BEA=90°,M、N分别是DC、AB的中点,
∴FM=$\frac{1}{2}$CD,EN=$\frac{1}{2}$AB,
∴FM=EN,
∴四边形EMFN是平行四边形.
点评 本题考查了平行四边形的判定及性质、全等三角形的判定及性质、平行线的判定及性质、直角三角形的性质,本题属于基础题,难度不大,在解决该题中,为了寻找一组相等的内错角借助了两次证明三角形全等稍显周折,在解决该题型题目时,根据全等三角形的性质去寻找相等的角去证平行是关键.

| A. | 45° | B. | 135° | C. | 50° | D. | 130° |
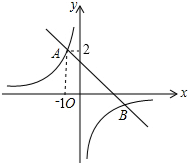 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )| A. | (-2,1) | B. | (2,1) | C. | (1,-2) | D. | (2,-1) |
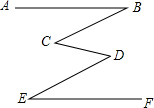 如图,已知AB∥EF,∠ABC=∠DEF,试判断BC和DE的位置关系,并说明理由.
如图,已知AB∥EF,∠ABC=∠DEF,试判断BC和DE的位置关系,并说明理由.