题目内容
8.在?ABCD中,对角线AC与BD相交于O,若AC=6,BD=10,则AD长度x的取值范是( )| A. | 2<x<6 | B. | 3<x<9 | C. | 1<x<9 | D. | 2<x<8 |
分析 根据平行四边形对角线互相平分可得OA=3,OD=4,再根据三角形的三边关系可得5-3<AD<5+3,即可得出结果.
解答 解:如图所示: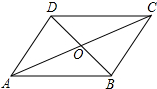
∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC=3,OD=$\frac{1}{2}$BD=5,
在△AOD中,由三角形的三边关系得:
∴5-3<AD<5+3,
即:2<x<8,
故选:D.
点评 此题主要考查了三角形的三边关系,以及平行四边形的性质;关键是掌握平行四边形的对角线互相平分.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
18.下列说法正确的是( )
| A. | 一个数的平方根一定是两个 | |
| B. | 一个正数的平方根一定是它的算术平方根 | |
| C. | 一个正数的算术平方根一定大于这个数的相反数 | |
| D. | 一个数的正的平方根是算术平方根 |
18.下列命题中假命题是( )
| A. | 两边及第三边上的高对应相等的两个三角形全等 | |
| B. | 两边及第三边上的中线对应相等的两个三角形全等 | |
| C. | 两边及两边的夹角对应相等的两个三角形全等 | |
| D. | 两边及其中一边上的中线对应相等的两个三角形全等 |
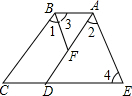 如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.
如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.
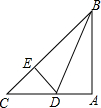 如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=20,则△DCE的周长为20.
如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=20,则△DCE的周长为20.