题目内容
16.一只不透明的袋子中装有1个红球、1个白球和1个黑球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,再从中任意摸出1个球,像这样有放回地先后摸球3次.求下列事件发生的概率:(1)3次摸到的球颜色都相同;
(2)3次摸到的球颜色都不相同.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与3次摸到的球颜色都相同情况,再利用概率公式即可求得答案;
(2)由(1)可求得3次摸到的球颜色都不相同的情况,再利用概率公式即可求得答案.
解答 解:(1)画树状图得:
∵共有27种等可能的结果,3次摸到的球颜色都相同有3种情况,
∴3次摸到的球颜色都相同的概率为:$\frac{3}{27}$=$\frac{1}{9}$;
(2)∵3次摸到的球颜色都不相同有6种情况,
∴3次摸到的球颜色都不相同的概率为:$\frac{6}{27}$=$\frac{2}{9}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 读图,完成图后的两个小题:
读图,完成图后的两个小题: 如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.
如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.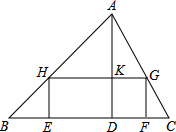 如图,在△ABC中,AD⊥BC于点D,矩形EFGH的四个顶点在三角形的三边上,已知BC=9cm,AD=8cm,EF=5cm,求矩形EFGH的面积.
如图,在△ABC中,AD⊥BC于点D,矩形EFGH的四个顶点在三角形的三边上,已知BC=9cm,AD=8cm,EF=5cm,求矩形EFGH的面积.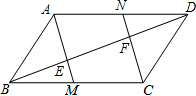 如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.
如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.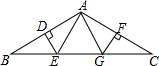 如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.
如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.