题目内容
7.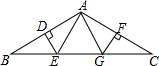 如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.
如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.
分析 利用线段的垂直平分线的性质得到:AE=BE,AG=CG,然后根据等边对等角得到:∠1=∠B,∠2=∠C,然后根据三角形内角和定理可得:∠1+∠2=60°,最后根据∠1+∠2+∠EAG=∠BAC,即可求∠EAG的度数,利用线段的垂直平分线的性质得到:AE=BE,AG=CG,就可以将△AEG的周长转化为线段BC的长.
解答  解:∵DE,FG分别是△ABC的边AB、AC的垂直平分线,
解:∵DE,FG分别是△ABC的边AB、AC的垂直平分线,
∴AE=BE,AG=CG,
∴∠1=∠B,∠2=∠C,
∵∠B+∠C+∠BAC=180°,∠BAC=120°,
∴∠B+∠C=60°,
∴∠1+∠2=60°,
∵∠1+∠2+∠EAG=∠BAC=120°,
∴∠EAG=60°;
(2)∵DE,FG分别是△ABC的边AB、AC的垂直平分线,
∴AE=BE,AG=CG,
∴△AEG的周长=AE+EG+AG=BE+EG+CG=BC=12,
∴△AEG的周长是12.
点评 题考查了线段的垂直平分线的性质,等腰三角形的性质,三角形的内角和,熟记线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.某件商品连续两次8折降价销售,降价后每件商品售价为a元,则该商品每件原价为( )
| A. | 0.64a | B. | $\frac{a}{0.8}$ | C. | $\frac{a}{0.64}$ | D. | 0.8a |
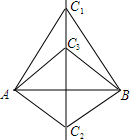 已知:如图,C1A=C1B,C2A=C2B.C3是直线C1C2上一点.求证:C3A=C3B.
已知:如图,C1A=C1B,C2A=C2B.C3是直线C1C2上一点.求证:C3A=C3B.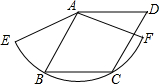 如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.
如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.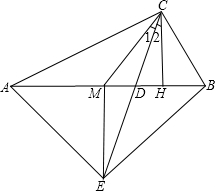 已知:如图,在Rt△ABC中,∠ACB=90°,点M是AB边的中点,CH⊥AB于点H,CD平分∠ACB.
已知:如图,在Rt△ABC中,∠ACB=90°,点M是AB边的中点,CH⊥AB于点H,CD平分∠ACB. 如图,在边长为2cm的正△ABC中,分别以A,B,C点为圆心,1cm长为半径作$\widehat{DE}$、$\widehat{EF}$、$\widehat{FD}$,求阴影部分的面积.
如图,在边长为2cm的正△ABC中,分别以A,B,C点为圆心,1cm长为半径作$\widehat{DE}$、$\widehat{EF}$、$\widehat{FD}$,求阴影部分的面积. 如图所示,在△ABC中,D、E、F分别为AB、AC、BC的中点,求证:△FED∽△ABC.
如图所示,在△ABC中,D、E、F分别为AB、AC、BC的中点,求证:△FED∽△ABC.