题目内容
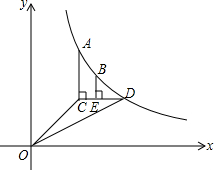 如图,已知函数y=
如图,已知函数y=| k |
| x |
(1)求△OCD的面积;
(2)当BE=AC时,求CE的长;
(3)在轴上是否存在一点P,使得PA+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
考点:反比例函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式,根据图象上的点满足函数解析式,可得D点坐标,根据三角形的面积公式,可得答案;
(2)根据BE的长,可得B点的纵坐标,根据点在函数图象上,可得B点横坐标,根据两点间的距离公式,可得答案;
(3)存在;分两种情况讨论:①当P在x轴上时,作点D关于x轴的对称点D′,连接AD′交x轴于P,PA+PD最小,∵PA+PD=AD′,根据勾股定理求出即可;②当P在y轴上时,作点A关于y轴的对称点A′,连接A′D交y轴于P,PA+PD最小,∵PA+PD=A′D,根据勾股定理求出即可.
(2)根据BE的长,可得B点的纵坐标,根据点在函数图象上,可得B点横坐标,根据两点间的距离公式,可得答案;
(3)存在;分两种情况讨论:①当P在x轴上时,作点D关于x轴的对称点D′,连接AD′交x轴于P,PA+PD最小,∵PA+PD=AD′,根据勾股定理求出即可;②当P在y轴上时,作点A关于y轴的对称点A′,连接A′D交y轴于P,PA+PD最小,∵PA+PD=A′D,根据勾股定理求出即可.
解答:
解:(1)∵y=
(x>0)的图象经过点A(1,2),
∴k=2,
∵AC∥y轴,AC=1,
∴点C的坐标为(1,1),
∵CD∥x轴,点D在函数图象上,
∴点D的坐标为(2,1),
∴S△OCD=
×1×1=
;
(2)∵BE=
AC,
∴BE=
,
∵BE⊥CD,
∴点B的纵坐标=2-
=
,
由反比例函数y=
,
得点B的横坐标为x=2÷
=
,
∴CE=
-1=
;
(3)存在;分两种情况讨论:如图所示: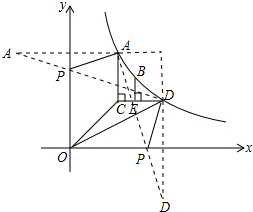
①当P在x轴上时,作点D关于x轴的对称点D′(2,1),
连接AD′交x轴于P,PA+PD最小;
∵PD′=PD,
∴PA+PD=AD′,
设直线AD′的解析式为y=kx+b,
把点A(1,2),D′(2,-1)代入得:
,
解得:k=-3,b=5,
∴y=-3x+5,
当y=0时,x=
,
∴P(
,0);
②当P在y轴上时,作点A关于y轴的对称点A′(-1,2),
连接A′D交y轴于P,PA+PD最小;
∵PA=PA′,
∴PA+PD=A′D,
设直线A′D的解析式为y=ax+c,
把A′(-1,2),D(2,1)代入得:
,
解得:a=-
,c=
,
∴y=-
x+
,
当x=0时,y=
,
∴P(0,
);
综上所述:点P坐标为(
,0)或(0,
).
| k |
| x |
∴k=2,
∵AC∥y轴,AC=1,
∴点C的坐标为(1,1),
∵CD∥x轴,点D在函数图象上,
∴点D的坐标为(2,1),
∴S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵BE=
| 1 |
| 2 |
∴BE=
| 1 |
| 2 |
∵BE⊥CD,
∴点B的纵坐标=2-
| 1 |
| 2 |
| 3 |
| 2 |
由反比例函数y=
| 2 |
| x |
得点B的横坐标为x=2÷
| 3 |
| 2 |
| 4 |
| 3 |
∴CE=
| 4 |
| 3 |
| 1 |
| 3 |
(3)存在;分两种情况讨论:如图所示:

①当P在x轴上时,作点D关于x轴的对称点D′(2,1),
连接AD′交x轴于P,PA+PD最小;
∵PD′=PD,
∴PA+PD=AD′,
设直线AD′的解析式为y=kx+b,
把点A(1,2),D′(2,-1)代入得:
|
解得:k=-3,b=5,
∴y=-3x+5,
当y=0时,x=
| 5 |
| 3 |
∴P(
| 5 |
| 3 |
②当P在y轴上时,作点A关于y轴的对称点A′(-1,2),
连接A′D交y轴于P,PA+PD最小;
∵PA=PA′,
∴PA+PD=A′D,
设直线A′D的解析式为y=ax+c,
把A′(-1,2),D(2,1)代入得:
|
解得:a=-
| 1 |
| 3 |
| 5 |
| 3 |
∴y=-
| 1 |
| 3 |
| 5 |
| 3 |
当x=0时,y=
| 5 |
| 3 |
∴P(0,
| 5 |
| 3 |
综上所述:点P坐标为(
| 5 |
| 3 |
| 5 |
| 3 |
点评:本题考查了反比例函数k的几何意义以及最短路程问题;利用待定系数法求反比例函数和一次函数的解析式,图象上的点满足函数解析式;通过作对称点找出满足最短路程的点是解决(3)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
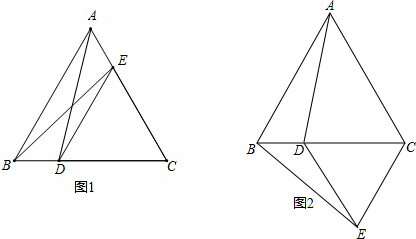
 农民王伯伯有一块地,如下图所示,已知:AB=90m,BC=120m,CD=130m,AD=140m,且∠B=90°.现在王伯伯年老力衰,要把地分给两个儿子,于是王伯伯以A、C两点划线,大儿子分得△ABC,小儿子分得△ADC.你认为王伯伯分法公平吗?请说明理由.
农民王伯伯有一块地,如下图所示,已知:AB=90m,BC=120m,CD=130m,AD=140m,且∠B=90°.现在王伯伯年老力衰,要把地分给两个儿子,于是王伯伯以A、C两点划线,大儿子分得△ABC,小儿子分得△ADC.你认为王伯伯分法公平吗?请说明理由. 如图所示,∠1=72°,∠2=50°,∠3=72°,求∠4的度数.
如图所示,∠1=72°,∠2=50°,∠3=72°,求∠4的度数. 如图,已知∠AOB=30°,P为∠AOB内一点,且OP=8.
如图,已知∠AOB=30°,P为∠AOB内一点,且OP=8.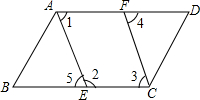 如图,根据图形完成下列填空.
如图,根据图形完成下列填空. 将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是
将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是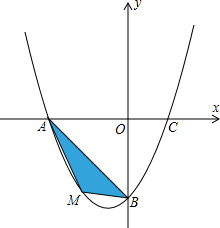 如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.
如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.