题目内容
已知:如图1,△ABC和△EDC都是等边三角形,点D、E分别在BC、AC上.
(1)填空:∠AED= = 度.
(2)求证:AD=BE.
(3)如图将图1中的△EDC沿BC所在直线翻折(如图2所示),其它条件不变,(2)中结论是否还成立?请说明理由.
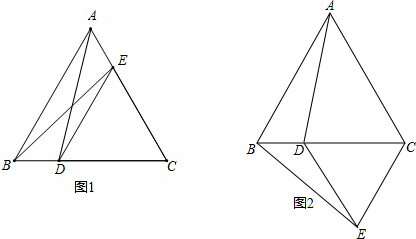
(1)填空:∠AED=
(2)求证:AD=BE.
(3)如图将图1中的△EDC沿BC所在直线翻折(如图2所示),其它条件不变,(2)中结论是否还成立?请说明理由.

考点:全等三角形的判定与性质,等边三角形的性质,翻折变换(折叠问题)
专题:
分析:(1)根据等边三角形的性质可得∠CED=∠CDE=60°,即可求得∠AED=∠BDE=120°;
(2)根据等边三角形的性质可得AC=BC,EC=DC.AC-EC=BC-DC,即AE=BD,再由(1)得知∠AED=∠BDE,ED为公共边,然后利用“边角边”证明△AED和△BDE全等,再根据全等三角形对应边相等证明即可;
(3)根据等边三角形的性质可得AC=BC,EC=DC,∠ACD=∠BCE=60°,然后利用“边角边”证明△ACD和△BCE全等,再根据全等三角形对应边相等证明即可.
(2)根据等边三角形的性质可得AC=BC,EC=DC.AC-EC=BC-DC,即AE=BD,再由(1)得知∠AED=∠BDE,ED为公共边,然后利用“边角边”证明△AED和△BDE全等,再根据全等三角形对应边相等证明即可;
(3)根据等边三角形的性质可得AC=BC,EC=DC,∠ACD=∠BCE=60°,然后利用“边角边”证明△ACD和△BCE全等,再根据全等三角形对应边相等证明即可.
解答:
解:(1)∵△EDC都是等边三角形,∴∠CED=∠CDE=60°,∴∠AED=∠BDE=120°
(2)证明:∵△ABC和△EDC都是等边三角形,∴AC=BC,EC=DC.∴AC-EC=BC-DC,即AE=BD.
在△AED和△BDE中,
,
∴△AED≌△BDE(SAS).
∴AD=BE.
(3)AD=BE仍成立;理由如下:
∵△ABC和△CDE都是等边三角形,
∴AC=BC,EC=DC,∠ACD=∠BCE=60°.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)证明:∵△ABC和△EDC都是等边三角形,∴AC=BC,EC=DC.∴AC-EC=BC-DC,即AE=BD.
在△AED和△BDE中,
|
∴△AED≌△BDE(SAS).
∴AD=BE.
(3)AD=BE仍成立;理由如下:
∵△ABC和△CDE都是等边三角形,
∴AC=BC,EC=DC,∠ACD=∠BCE=60°.
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE.
点评:本题考查了全等三角形的判定与性质、等边三角形的性质以及翻折变换;熟记等边三角形的性质以及全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
下列给出的四个结论中,说法正确的有( )
①射线OA与射线AO是同一条射线 ②若AP=BP,则点P是线段AB的中点
③数轴上表示数3和-3的点到原点的距离相等 ④若a2=9,则a一定等于3.
①射线OA与射线AO是同一条射线 ②若AP=BP,则点P是线段AB的中点
③数轴上表示数3和-3的点到原点的距离相等 ④若a2=9,则a一定等于3.
| A、1个 | B、2个 | C、3个 | D、4个 |
平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
| A、只有① | B、只有② |
| C、①②都正确 | D、①②都不正确 |
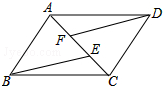 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.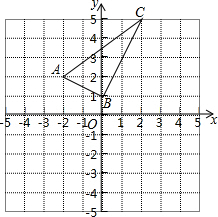 如图,直角坐标系中的网格由单位正方形组成,三角形ABC中,C点坐标为(2,5).
如图,直角坐标系中的网格由单位正方形组成,三角形ABC中,C点坐标为(2,5).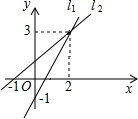 如图中两直线l1,l2的交点坐标可以看作方程组
如图中两直线l1,l2的交点坐标可以看作方程组 如图,已知函数y=
如图,已知函数y=