题目内容
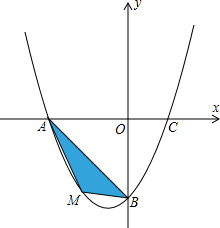 如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.
如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形(要求PQ∥OB),直接写出相应的点Q的坐标.
考点:二次函数综合题
专题:
分析:(1)根据抛物线与x轴的交点A与C坐标设出抛物线的解析式方程,将B坐标代入即可确定出解析式;
(2)过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积-三角形AOB面积,求出即可;
(3)根据题意设p(a,
a2+a-4),则Q(a,-a),分两种情况分别讨论即可求得.
(2)过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积-三角形AOB面积,求出即可;
(3)根据题意设p(a,
| 1 |
| 2 |
解答:
解:(1)设抛物线解析式为y=a(x+4)(x-2),
将B(0,-4)代入得:-4=-8a,即a=
,
则抛物线解析式为y=
(x+4)(x-2)=
x2+x-4;
(2)过M作MN⊥x轴,
将x=m代入抛物线得:y=
m2+m-4,即M(m,
m2+m-4),
∴MN=|
m2+m-4|=-
m2-m+4,ON=-m,
∵A(-4,0),B(0,-4),
∴OA=OB=4,
∴△AMB的面积为S=S△AMN+S梯形MNOB-S△AOB
=
×(4+m)×(-
m2-m+4)+
×(-m)×(-
m2-m+4+4)-
×4×4
=2(-
m2-m+4)-2m-8
=-m2-4m
=-(m+2)2+4,
当m=-2时,S取得最大值,最大值为4;
(3)如果使以点P、Q、B、O为顶点的四边形为平行四边形(要求PQ∥AB),则PQ=OB,
设p(a,
a2+a-4),则Q(a,-a),如图,

①当点P在点Q上面时,则
a2+a-4-(-a)=4,
解得a=-2+2
或a=-2-2
,
∴Q(-2+2
,2-2
)或(-2-2
,2+2
).
②当点Q在点P上面时,-a-(
a2+a-4)=4,
解得a=0或a=-4,
∴Q(-4,4);
综上,有三个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,相应的点Q的坐标为(-4,4)或(-2+2
,2-2
)或(-2-2
,2+2
).
将B(0,-4)代入得:-4=-8a,即a=
| 1 |
| 2 |
则抛物线解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过M作MN⊥x轴,
将x=m代入抛物线得:y=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=|
| 1 |
| 2 |
| 1 |
| 2 |
∵A(-4,0),B(0,-4),
∴OA=OB=4,
∴△AMB的面积为S=S△AMN+S梯形MNOB-S△AOB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=2(-
| 1 |
| 2 |
=-m2-4m
=-(m+2)2+4,
当m=-2时,S取得最大值,最大值为4;
(3)如果使以点P、Q、B、O为顶点的四边形为平行四边形(要求PQ∥AB),则PQ=OB,
设p(a,
| 1 |
| 2 |

①当点P在点Q上面时,则
| 1 |
| 2 |
解得a=-2+2
| 5 |
| 5 |
∴Q(-2+2
| 5 |
| 5 |
| 5 |
| 5 |
②当点Q在点P上面时,-a-(
| 1 |
| 2 |
解得a=0或a=-4,
∴Q(-4,4);
综上,有三个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,相应的点Q的坐标为(-4,4)或(-2+2
| 5 |
| 5 |
| 5 |
| 5 |
点评:此题考查了二次函数综合题,涉及的知识有:待定系数法求抛物线解析式,坐标与图形性质,三角形及梯形的面积求法,以及二次函数的性质,熟练掌握二次函数的图象与性质是解本题的关键,在求有关动点问题时要注意分析题意分情况讨论求得结果.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
计算(-x)2•x3的结果为( )
| A、x5 |
| B、x6 |
| C、-x6 |
| D、-x5 |
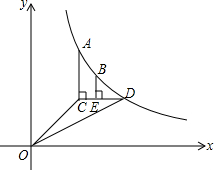 如图,已知函数y=
如图,已知函数y= 画出如图所示立体图形的三视图.
画出如图所示立体图形的三视图.