题目内容
 如图,已知∠AOB=30°,P为∠AOB内一点,且OP=8.
如图,已知∠AOB=30°,P为∠AOB内一点,且OP=8.(1)用直尺和圆规作出P点关于直线OA的对称点M,P点关于直线OB的对称点N;(保留作图痕迹,不写作法)
(2)连接OM、ON、MN,求∠MON的度数;
(3)线段MN的长度为
考点:作图-轴对称变换
专题:
分析:(1)利用对称点的定义进而判断得出即可;
(2)利用轴对称的性质进而求出即可;
(3)利用等边三角形的判定与性质求出即可.
(2)利用轴对称的性质进而求出即可;
(3)利用等边三角形的判定与性质求出即可.
解答:
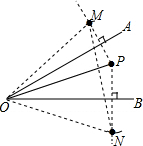 解:(1)如图所示:M,N即为所求;
解:(1)如图所示:M,N即为所求;
(2)∵P点关于直线OA的对称点M,P点关于直线OB的对称点N,
∴OM=OP,OP=ON,∠MOA=∠AOP,∠POB=∠BON,
∴∠MON的度数为:2∠AOB=2×30°=60°;
(3)由(2)得:∠MON=60°,OM=ON,故△MON是等边三角形,故OP=MN=MO=8.
故答案为:8.
 解:(1)如图所示:M,N即为所求;
解:(1)如图所示:M,N即为所求;(2)∵P点关于直线OA的对称点M,P点关于直线OB的对称点N,
∴OM=OP,OP=ON,∠MOA=∠AOP,∠POB=∠BON,
∴∠MON的度数为:2∠AOB=2×30°=60°;
(3)由(2)得:∠MON=60°,OM=ON,故△MON是等边三角形,故OP=MN=MO=8.
故答案为:8.
点评:此题主要考查了轴对称变换以及等边三角形的判定与性质,得出△MON是等边三角形是解题关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
| A、只有① | B、只有② |
| C、①②都正确 | D、①②都不正确 |
如果AD是△ABC的中线,那么下列结论一定成立的有( )
①BD=CD;②AB=AC;③S△ABD=
S△ABC.
①BD=CD;②AB=AC;③S△ABD=
| 1 |
| 2 |
| A、3个 | B、2个 | C、1个 | D、0个 |
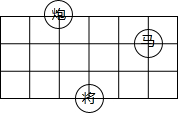 如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )
如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )| A、(0,0) |
| B、(-2,-2) |
| C、(0,-2) |
| D、(-2,-3) |
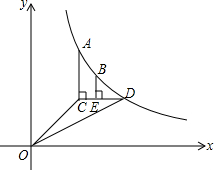 如图,已知函数y=
如图,已知函数y=
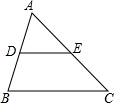 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠C=40°.
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠C=40°.