题目内容
6.不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1>0}\\{x-2≤0}\end{array}\right.$的解集在数轴上可表示为( )| A. | 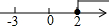 | B. |  | C. | 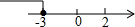 | D. |  |
分析 分别求出每一个不等式的解集,根据口诀:大小小大中间找,确定不等式组的解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则可得答案.
解答 解:解不等式$\frac{1}{3}$x+1>0,得:x>-3,
解不等式x-2≤0,得:x≤2,
∴不等式组的解集为:-3<x≤2,
故选:D.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
16.下列四个数中,最小的数是( )
| A. | |-2| | B. | 0 | C. | |1| | D. | -3 |
 如图,△ABC为等边三角形,CA⊥x轴,S△ABC=6,双曲线y=$\frac{k}{x}$经过点A、B,则k的值为12.
如图,△ABC为等边三角形,CA⊥x轴,S△ABC=6,双曲线y=$\frac{k}{x}$经过点A、B,则k的值为12. 如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)
如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)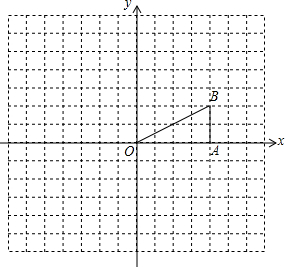 如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).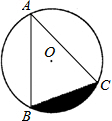 如图,点A、B、C在直径为4$\sqrt{3}$的⊙O上,∠BAC=45°,则图中阴影部分的面积等于3π-6(结果保留π).
如图,点A、B、C在直径为4$\sqrt{3}$的⊙O上,∠BAC=45°,则图中阴影部分的面积等于3π-6(结果保留π).