题目内容
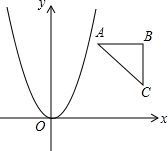
17. 如图,△ABC为等边三角形,CA⊥x轴,S△ABC=6,双曲线y=$\frac{k}{x}$经过点A、B,则k的值为12.
如图,△ABC为等边三角形,CA⊥x轴,S△ABC=6,双曲线y=$\frac{k}{x}$经过点A、B,则k的值为12.
分析 设点A的坐标为(m,n)(n>0),根据等边三角形的性质找出点B的坐标,由A、B点均在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出m、n间的关系,再结合三角形的面积公式即可得出n2的值,将其代入k=mn中即可得出结论.
解答 解:设点A的坐标为(m,n)(n>0),
∵CA⊥x轴,△ABC为等边三角形,
∴点B的坐标为(m+$\frac{\sqrt{3}}{2}$n,$\frac{1}{2}$n).
∵点A、B均在反比例函数y=$\frac{k}{x}$的图象上,
∴k=mn=(m+$\frac{\sqrt{3}}{2}$n)$\frac{1}{2}$n,即m=$\frac{\sqrt{3}}{2}$n.
∵S△ABC=$\frac{1}{2}$AC•(xB-xA)=$\frac{1}{2}$n×$\frac{\sqrt{3}}{2}$n=6,
解得:n2=8$\sqrt{3}$.
∵k=mn=$\frac{\sqrt{3}}{2}$n2=$\frac{\sqrt{3}}{2}$×8$\sqrt{3}$=12.
故答案为:12.
点评 本题考查了等边三角形的性质、反比例函数图象上点的坐标特征以及三角形的面积公式,解题的关键是找出m、n之间的关系.本题属于基础题,难度不大,解决该题型题目时,设出等边三角形的一个顶点的坐标为(m,n),结合等边三角形的性质找出另一个顶点的坐标,结合反比例函数图象上点的坐标特征找出m、n、k之间的关系是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
5.为了了解某区的绿化进程,小明同学查询了园林绿化政务网,根据网站发布的近几年该城市城市绿化资源情况的相关数据,绘制了如下统计图(不完整)
某市2011-2015年人均公共绿地面积年增长率统计图 某市2011-2015年人均公共绿地面积统计图
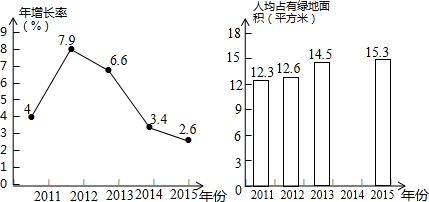
(1)请根据以上信息解答下列问题:
①求2014年该市人均公共绿地面积是多少平方米(精确到0.1)?
②补全条形统计图:
(2)小明同学还了解到自己身边的许多同学都树立起了绿色文明理念,从自身做起,多种树,为提高人均公共绿地面积做贡献,他对所在班级的40多名同学2015年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
如果按照小明的统计数据,请你通过计算估计,他所在学校的300名同学在2015年共植树多少棵?
某市2011-2015年人均公共绿地面积年增长率统计图 某市2011-2015年人均公共绿地面积统计图

(1)请根据以上信息解答下列问题:
①求2014年该市人均公共绿地面积是多少平方米(精确到0.1)?
②补全条形统计图:
(2)小明同学还了解到自己身边的许多同学都树立起了绿色文明理念,从自身做起,多种树,为提高人均公共绿地面积做贡献,他对所在班级的40多名同学2015年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
| 种树棵数(棵) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 10 | 5 | 6 | 9 | 4 | 6 |
2.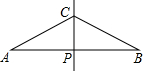 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
| A. | 甲、乙都正确 | B. | 甲、乙都错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
7.若x=5是关于x的方程2x+3m-1=0的解,则m的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |

 已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.