题目内容
1.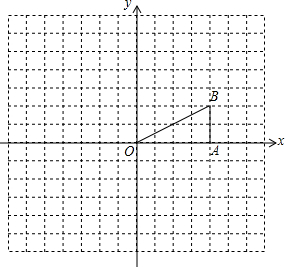 如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).(1)画出△OAB向下平移3个单位后的△O1A1B1;
(2)画出△OAB绕点O逆时针旋转90°后的△OA2B2;
(3)求点B旋转到点B2所经过的路线长(结果保留根号和π)
分析 (1)利用点平移的坐标规律,分别写出点O、A、B平移后所对应的点O1、A1、B1的坐标,然后描点即可得到△O1A1B1;
(2)利用网格特点和旋转的性质,分别画出点A、B的对应的点A2、B2,即可得到△OA2B2;
(3)先利用勾股定理计算出OB,然后根据弧长公式求解.
解答 解:(1)如图,△O1A1B1 为所作;
(2)任意,△OA2B2为所作;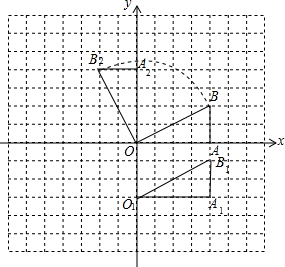
(2)OB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
所以点B旋转到点B2所经过的路线长=$\frac{90•π•2\sqrt{5}}{180}$=$\sqrt{5}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
13.下列运算正确的是( )
| A. | x4+x4=x8 | B. | (x-y)2=x2-y2 | C. | x3•x4=x7 | D. | (2x2)3=2x6 |
10.已知一个正n边形的每个内角为120°,则这个多边形的对角线有( )
| A. | 5条 | B. | 6条 | C. | 8条 | D. | 9条 |
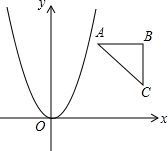 已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$. 如图,直线y=kx与双曲线y=-$\frac{2}{x}$交于A(x1,y1),B(x2,y2)两点,则2x1y2-8x2y1的值为( )
如图,直线y=kx与双曲线y=-$\frac{2}{x}$交于A(x1,y1),B(x2,y2)两点,则2x1y2-8x2y1的值为( )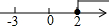

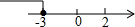

 (1)解不等式组$\left\{\begin{array}{l}{2x+1<7}\\{3-x≤4}\end{array}\right.$并把解集在数轴上表示出来.
(1)解不等式组$\left\{\begin{array}{l}{2x+1<7}\\{3-x≤4}\end{array}\right.$并把解集在数轴上表示出来.