题目内容
18.(1)计算:2sin30°+$\sqrt{2}$•$\sqrt{8}$-(2-π)0-($\frac{1}{2}$)-1(2)解方程:$\frac{1}{x}$+$\frac{3}{x-2}$=$\frac{2}{2x-{x}^{2}}$.
分析 (1)分别利用零指数幂的性质和特殊角的三角函数值、二次根式的性质分别化简求出答案;
(2)首先找出最简公分母,进而去分母得出答案.
解答 解:(1)2sin30°+$\sqrt{2}$•$\sqrt{8}$-(2-π)0-($\frac{1}{2}$)-1
=2×$\frac{1}{2}$+4-1-2
=2;
(2)去分母得:x-2+3x=-2,
解得:x=0,
检验:当x=0时,x(x-2)=0,故此方程无实数根.
点评 此题主要考查了零指数幂的性质和特殊角的三角函数值、二次根式的性质、分式方程的解法等知识,正确把握相关性质是解题关键.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | x4+x4=x8 | B. | (x-y)2=x2-y2 | C. | x3•x4=x7 | D. | (2x2)3=2x6 |
10.已知一个正n边形的每个内角为120°,则这个多边形的对角线有( )
| A. | 5条 | B. | 6条 | C. | 8条 | D. | 9条 |
7.若x=5是关于x的方程2x+3m-1=0的解,则m的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |

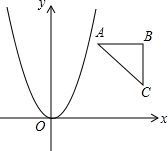 已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.