题目内容
14. 如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)
如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)
分析 先证明△ODB是等边三角形,得到∠DOB=60°,根据弧长公式即可解决问题.
解答 解:连结OD, ∵△BCD是由△BCO翻折得到,
∵△BCD是由△BCO翻折得到,
∴∠CBD=∠CBO,∠BOD=∠BDO,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠ODB=2∠DBC,
∵∠ODB+∠DBC=90°,
∴∠ODB=60°,
∵OD=OB
∴△ODB是等边三角形,
∴∠DOB=60°,
∵∠AOB=110°,
∴∠AOD=∠AOB-∠DOB=50°,
∴弧AD的长=$\frac{50π×18}{180}$=5π.
故答案为:5π.
点评 本题考查翻折变换、弧长公式、等边三角形的判定和性质等知识,解题的关键是等边三角形的发现,属于中考常考题型.

练习册系列答案
相关题目
5.为了了解某区的绿化进程,小明同学查询了园林绿化政务网,根据网站发布的近几年该城市城市绿化资源情况的相关数据,绘制了如下统计图(不完整)
某市2011-2015年人均公共绿地面积年增长率统计图 某市2011-2015年人均公共绿地面积统计图
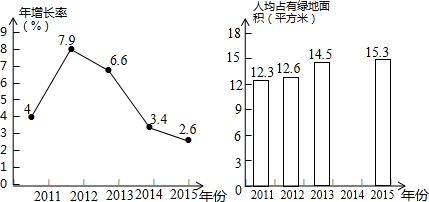
(1)请根据以上信息解答下列问题:
①求2014年该市人均公共绿地面积是多少平方米(精确到0.1)?
②补全条形统计图:
(2)小明同学还了解到自己身边的许多同学都树立起了绿色文明理念,从自身做起,多种树,为提高人均公共绿地面积做贡献,他对所在班级的40多名同学2015年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
如果按照小明的统计数据,请你通过计算估计,他所在学校的300名同学在2015年共植树多少棵?
某市2011-2015年人均公共绿地面积年增长率统计图 某市2011-2015年人均公共绿地面积统计图

(1)请根据以上信息解答下列问题:
①求2014年该市人均公共绿地面积是多少平方米(精确到0.1)?
②补全条形统计图:
(2)小明同学还了解到自己身边的许多同学都树立起了绿色文明理念,从自身做起,多种树,为提高人均公共绿地面积做贡献,他对所在班级的40多名同学2015年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
| 种树棵数(棵) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 10 | 5 | 6 | 9 | 4 | 6 |
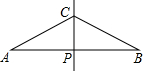 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法: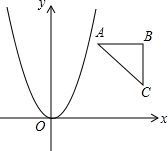 已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.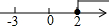

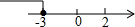

 如图,在矩形ABCD中,E、F分别在AB、CD上,且DE=BF.求证:四边形DEBF是平行四边形.
如图,在矩形ABCD中,E、F分别在AB、CD上,且DE=BF.求证:四边形DEBF是平行四边形.