题目内容
6．下列多项式中，能用公式法因式分解的是（ ）| A． | -a2-b2 | B． | a2+b2 | C． | -4a2+12ab-9 | D． | 25m2+15n+9 |
分析 根据：能够运用平方差公式分解因式的多项式必须是二项式，两项都能写成平方的形式，且符号相反．
能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍进行分析即可．
解答 解：A、-a2-b2=-（a2+b2），不符合平方差公式，故此选项错误；
B、a2+b2不符合平方差公式，故此选项错误；
C、-4a2+12ab-9=-（2a-3）2，故此选项正确；
D、25m2+15n+9中间15n不是两项乘积的2倍，不符合完全平方公式特点，故此选项错误；
故选：C．
点评 此题主要考查了公式法分解因式，关键是掌握能够运用平方差公式和完全平方公式分解因式的多项式的特点．
练习册系列答案
相关题目
16．下列方程组中，不是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{2x-5y=8}\\{x=y}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=1}\\{x=y+z}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |
14．不等式$-\frac{1}{2}≤\frac{1-0.6x}{-3}≤\frac{2}{3}$的整数解的个数为（ ）
| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
11．使分式$\frac{x+3}{2x-8}$有意义的x值是（ ）
| A． | x=4 | B． | x=-3 | C． | x≠4 | D． | x=≠-3 |
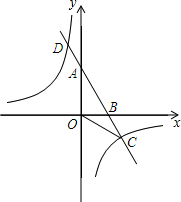如图，已知A，B两点的坐标分别是A（0，2$\sqrt{3}$），B（2，0），直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D（-1，a）．
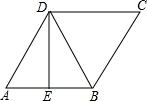如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，求∠ABD的度数．