题目内容
7.在Rt△ABC中,∠C=90°,BC=2,Rt△ABC绕着点B按顺时针方向旋转,使点C落在斜边AB上的点D处,设点A旋转后与点E重合,连接AE,过点E作直线EM与射线CB垂直,交点为M.(1)若点M与点B重合,如图1,求cot∠BAE的值;
(2)若点M在边BC上如图2,设边长AC=x,BM=y,点M不与点B重合,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)若∠BAE=∠EBM,求斜边AB的长.
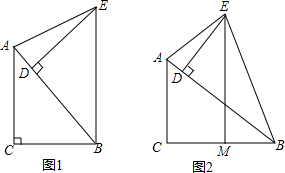
分析 (1)由旋转有,BC=BD=2,AC=ED,∠CBA=∠EBD=∠C=90°,通过计算出AC=CB=2,AB=2$\sqrt{2}$,DE=DB=2,即可;
(2)由(1)中的结论得出△EDG∽△BDE,再由cos∠ABC=$\frac{MB}{BG}=\frac{BC}{AB}$,建立函数关系;
(3)由旋转有,AB=EB,∠AEB=∠BAE,∠CBA=x经过简单的计算出:HC=BC=2,HB=HE=4,∠CBA=60°即可.
解答 解:(1)由旋转有,BC=BD=2,AC=ED,∠CBA=∠EBD=∠C=90°,
∵EM⊥CB,
∴∠EBC=90°,
∴∠CBA=∠EBD=45°,
∴AC=CB=2,
∴AB=2$\sqrt{2}$,
∵DE=DB=2,
∴AD=AB-BD=2$\sqrt{2}$-2,
∴cot∠BAE=$\frac{AD}{DE}$=$\sqrt{2}$-1,
(2)设EM与边AB交于G,
由(1)有∠DEM+∠DGE=90°,∠BGM+∠ABM=90°,∠DGE=∠BGM,
∴∠DEM=∠CBA,∠EBD=∠CBA,
∴∠DEM=∠EBD,∠EDG=∠BDE,
∴△EDG∽△BDE,
∴$\frac{ED}{BD}=\frac{DG}{ED}$,
∵BC=BD=2,AC=ED=x,
∴$\frac{x}{2}=\frac{DG}{x}$,
∴DG=$\frac{{x}^{2}}{2}$,
∵cos∠ABC=$\frac{MB}{BG}=\frac{BC}{AB}$,
∴AB=$\sqrt{{x}^{2}+4}$,GB=$\frac{4-{x}^{2}}{2}$,
∴$\frac{y}{\frac{4-{x}^{2}}{2}}=\frac{2}{\sqrt{{x}^{2}+4}}$,
∴y=$\frac{4-{x}^{2}}{{x}^{2}+4}\sqrt{{x}^{2}+4}$(0<x<2)
(3)延长EA,BC交于H,如图1,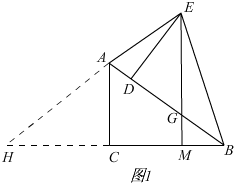
由旋转有,AB=EB,∠AEB=∠BAE,∠CBA=x
∴∠ABE=x,∠BAE=∠EBM,
∴∠AEB=∠BAE=∠EBM=2x,
∵∠ABE+∠BAE+∠AEB=180°,
∴x=36°,
∴∠H=∠ABH=∠ABE=36°,
∠HBE=∠BAE=∠AEB=72°,
∴AH=AB=BE,HB=HE,
∵∠ACB=90°
∴HC=BC=2,
∴HB=HE=4,
∴△BAE∽△HBE,
∴$\frac{AB}{HB}=\frac{AE}{BE}$,
∵BE=AB,
∴AE=HE-HA=4-AB,
∴$\frac{AB}{4}=\frac{4-AB}{AB}$,
∴AB=-2+2$\sqrt{5}$或AB=-2-2$\sqrt{5}$(舍),
当点M在CB延长线时,如图2,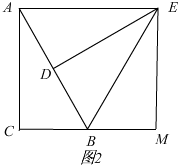
∵∠AEB=∠BAE=∠EBM,
∴∠AEB=∠EBM,
∴AE∥MC,
∴∠BAE=∠CBA,
∵∠CBA=∠EBA,
∴∠EBM=∠CBA=∠EBA,
∴∠CBA=60°,
∵cos∠CBA=$\frac{BC}{AB}$,
∴BC=2,
∴AB=4,
即:AB=-2+2$\sqrt{5}$或4.
点评 此题是几何变换综合题,主要考查了平移,旋转的性质,三角函数相似三角形的性质和判定,由平移,旋转得出结论是解本题的关键.

| A. | -a2-b2 | B. | a2+b2 | C. | -4a2+12ab-9 | D. | 25m2+15n+9 |
部分时段车流量情况调查表
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6:30~7:00 | ①② | 2747 | 92 |
| 中午放学11:20~11:50 | ③④ | 1449 | 48 |
| 下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
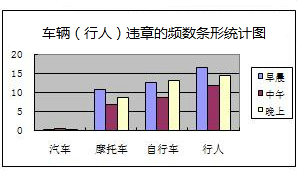 回答下列问题:
回答下列问题:(1)请你写出2条交通法规:①红灯停、绿灯行,②过马路要走人行横道线;
(2)早晨、中午、晚上三个时段每分钟车流量的极差是74,这三个时段的车流总量的中位数是2747;
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因;
(4)通过分析写一条合理化建议.
| A. | $\frac{1}{a{b}^{2}}$$\sqrt{ab}$ | B. | $\frac{1}{{a}^{2}b}$$\sqrt{ab}$ | C. | $\frac{1}{b}\sqrt{ab}$ | D. | b$\sqrt{ab}$ |
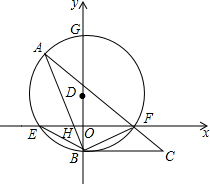 如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.
如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.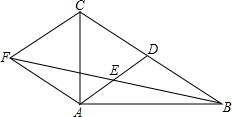 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
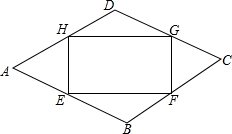 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.