题目内容
1.若(x2+px+8)•(x2-3x+1)的结果中不含x3项,则P=3.分析 先根据多项式乘以多项式法则展开,合并后即可得出方程,求出方程的解即可.
解答 解:(x2+px+8)•(x2-3x+1)
=x4-3x3+x2+px3-3px2+px+8x2-24x+8
=x4+(-3+p)x3+(9-3p)x2+(p-24)x+8,
∵(x2+px+8)•(x2-3x+1)的结果中不含x3项,
∴-3+p=0,
解得:p=3,
故答案为:3.
点评 本题考查了多项式乘以多项式法则的应用,能正确根据多项式乘以多项式法则展开是解此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
6.下列多项式中,能用公式法因式分解的是( )
| A. | -a2-b2 | B. | a2+b2 | C. | -4a2+12ab-9 | D. | 25m2+15n+9 |
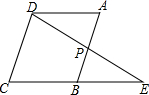 如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.
如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD. 如图,E、F、G、H分别是?ABCD各边的中点.
如图,E、F、G、H分别是?ABCD各边的中点.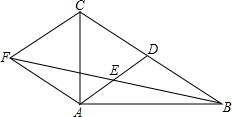 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
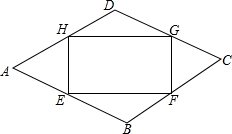 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.