题目内容
 如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF.
如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF.考点:平行四边形的性质
专题:证明题
分析:首先根据平行四边形的性质可得AD=CB,AD∥CB,AO=CO,然后再证明△AOF≌△COE可得AF=CE,再利用等式的性质可得BE=DF.
解答:证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,AO=CO,
∴∠F=∠E,
在△AOF和△COE中
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF-AD=CE-CB,
即DF=BE.
∴AD=CB,AD∥CB,AO=CO,
∴∠F=∠E,
在△AOF和△COE中
|
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF-AD=CE-CB,
即DF=BE.
点评:此题主要考查了平行四边形的性质,关键是掌握平行四边形的对角线互相平分,对边相等.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,四边形ABCD和四边形AEFG是正方形,△AED是等边三角形,则图中度数为30°的角有( )
如图,四边形ABCD和四边形AEFG是正方形,△AED是等边三角形,则图中度数为30°的角有( )| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,若AB=10,则图中阴影部分的面积为( )
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,若AB=10,则图中阴影部分的面积为( )| A、100π | B、75π |
| C、50π | D、25π |
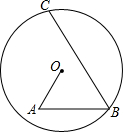 如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB=
如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB= 如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,写出y与x的函数关系式.
如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,写出y与x的函数关系式. 如图,在△ABC中,点D在BC上,BD:DC=1:2,点E在AB上,AE:EB=3:2,AD,CE相交于F,则AF:FD=
如图,在△ABC中,点D在BC上,BD:DC=1:2,点E在AB上,AE:EB=3:2,AD,CE相交于F,则AF:FD= 如图,四边形ABCD是矩形,四边形AECF是菱形,若AB=4,BC=8,求菱形AECF的面积.
如图,四边形ABCD是矩形,四边形AECF是菱形,若AB=4,BC=8,求菱形AECF的面积.
 求阴影部分面积.
求阴影部分面积.